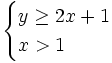Plantilla:Sistemas de inecuaciones lineales con dos incógnitas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:02 15 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:09 28 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Caja Amarilla|texto=*Un '''sistema de inecuaciones lineales con dos incógnitas''' es un conjunto de inecuaciones lineales con una incógnita. | {{Caja Amarilla|texto=*Un '''sistema de inecuaciones lineales con dos incógnitas''' es un conjunto de inecuaciones lineales con una incógnita. | ||
| - | * Una '''solución''' de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.}} | + | * Una '''solución''' de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente. |
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=1´19" | ||
| + | |url1=https://youtu.be/urgAaz76etc | ||
| + | |sinopsis=Determina si el punto (2,5) es solución del sistema | ||
| + | |||
| + | :<math>\begin{cases}y \ge 2x+1 \\ x>1\end{cases}</math> | ||
| + | }} | ||
Revisión de 18:09 28 dic 2017
- Un sistema de inecuaciones lineales con dos incógnitas es un conjunto de inecuaciones lineales con una incógnita.
- Una solución de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.
Determina si el punto (2,5) es solución del sistema