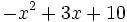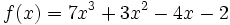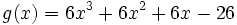Plantilla:Videotutoriales factorizacion Ruffini
De Wikipedia
| Revisión de 17:53 2 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 4: | Línea 4: | ||
| |duracion=26'17" | |duracion=26'17" | ||
| |sinopsis=Método que nos permite factorizar polinomios de grado mayor que dos. | |sinopsis=Método que nos permite factorizar polinomios de grado mayor que dos. | ||
| - | |url1=https://www.youtube.com/watch?v=hzfOZ7_2FNk&index=11&list=PLZNmE9BEzVImKUDFE-SsTXvB2FiwalKLM | + | |url1=http://www.youtube.com/watch?v=hzfOZ7_2FNk&index=11&list=PLZNmE9BEzVImKUDFE-SsTXvB2FiwalKLM |
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Tutorial 2 | |titulo1=Tutorial 2 | ||
| |duracion=9´55" | |duracion=9´55" | ||
| - | |url1=https://www.youtube.com/watch?v=OkI-luzzUjc&list=PL54E0E2B3C3F7EA2B&index=14 | + | |url1=http://www.youtube.com/watch?v=OkI-luzzUjc&list=PL54E0E2B3C3F7EA2B&index=14 |
| |sinopsis=*'''Factorizar''' un polinomio P(x) es expresarlo como producto de otros de menor grado que él, y para ello hay que calcular los "ceros" de P(x), cosa no siempre fácil. | |sinopsis=*'''Factorizar''' un polinomio P(x) es expresarlo como producto de otros de menor grado que él, y para ello hay que calcular los "ceros" de P(x), cosa no siempre fácil. | ||
| *Si "a" es un "cero" de P(x) y C(x) es el cociente de la división P(x)/(x-a), entonces P(x) = (x-a).C(x). | *Si "a" es un "cero" de P(x) y C(x) es el cociente de la división P(x)/(x-a), entonces P(x) = (x-a).C(x). | ||
| Línea 19: | Línea 19: | ||
| |duracion=9'19" | |duracion=9'19" | ||
| |sinopsis=Cómo hacer una descomposición factorial de polinomios por Ruffini. | |sinopsis=Cómo hacer una descomposición factorial de polinomios por Ruffini. | ||
| - | |url1=https://www.youtube.com/watch?v=jZyodblJV-0&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=3 | + | |url1=http://www.youtube.com/watch?v=jZyodblJV-0&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=3 |
| }} | }} | ||
| ---- | ---- | ||
| Línea 56: | Línea 56: | ||
| :<math>g(x)=6x^3+6x^2+6x-26\;</math> | :<math>g(x)=6x^3+6x^2+6x-26\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=2CY0oR_UqfA | + | |url1=http://www.youtube.com/watch?v=2CY0oR_UqfA |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 66: | Línea 66: | ||
| :8b) <math>x^2-4x+4\;</math> | :8b) <math>x^2-4x+4\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=uJhwKHxOAu0&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=23 | + | |url1=http://www.youtube.com/watch?v=uJhwKHxOAu0&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=23 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 76: | Línea 76: | ||
| :8d) <math>x^2+6x+9\;</math> | :8d) <math>x^2+6x+9\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=yQiCsQq7_Ao&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=24 | + | |url1=http://www.youtube.com/watch?v=yQiCsQq7_Ao&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=24 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 86: | Línea 86: | ||
| :8f) <math>x^2-10x+25\;</math> | :8f) <math>x^2-10x+25\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=qVBx3s2hcWc&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=25 | + | |url1=http://www.youtube.com/watch?v=qVBx3s2hcWc&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=25 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 96: | Línea 96: | ||
| :8h) <math>2x^2+2x-4\;</math> | :8h) <math>2x^2+2x-4\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=xSC-dIcc1cg&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=26 | + | |url1=http://www.youtube.com/watch?v=xSC-dIcc1cg&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=26 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 106: | Línea 106: | ||
| :8j) <math>x^2+3x+2\;</math> | :8j) <math>x^2+3x+2\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=vr8c0kynzCM&index=27&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9 | + | |url1=http://www.youtube.com/watch?v=vr8c0kynzCM&index=27&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 116: | Línea 116: | ||
| :8l) <math>-x^2+3x+10\;</math> | :8l) <math>-x^2+3x+10\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=Qx45ZHpPMxM&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=28 | + | |url1=http://www.youtube.com/watch?v=Qx45ZHpPMxM&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=28 |
| }} | }} | ||
| }} | }} | ||
Revisión actual
Método que nos permite factorizar polinomios de grado mayor que dos.
- Factorizar un polinomio P(x) es expresarlo como producto de otros de menor grado que él, y para ello hay que calcular los "ceros" de P(x), cosa no siempre fácil.
- Si "a" es un "cero" de P(x) y C(x) es el cociente de la división P(x)/(x-a), entonces P(x) = (x-a).C(x).
- Teorema de la factorización: si los coeficientes de un polinomio P(x) son números enteros, los ceros enteros de P(x) son divisores del término independiente de P(x).
- Si la suma de los coeficientes de P(x) es 0, pues apostar tranquilamente la vida a que el número 1 es un "cero" de P(x); o sea, P(x) es divisible por (x-1).
Cómo hacer una descomposición factorial de polinomios por Ruffini.
Factoriza los polinomios:
- a)
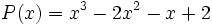
- b)
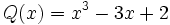
Factoriza el polinomio 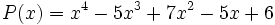
Factoriza el polinomio 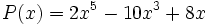
Factoriza el polinomio 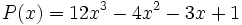 sabiendo que sólo tiene raíces fraccionarias.
sabiendo que sólo tiene raíces fraccionarias.
Hallar los puntos de intersección de las dos funciones polinómicas siguientes:
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8a)
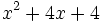
- 8b)
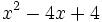
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8c)
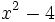
- 8d)
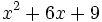
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8e)
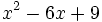
- 8f)
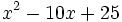
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8g)
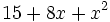
- 8h)
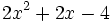
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8i)
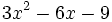
- 8j)
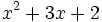
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8k)
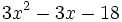
- 8l)