Vectores en el plano (4ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:20 14 sep 2019 Coordinador (Discusión | contribuciones) (→Vectores en el plano) ← Ir a diferencia anterior |
Revisión de 14:47 14 sep 2019 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 46: | Línea 46: | ||
| |sinopsis=Tipos de vectores: vector director, vector opuesto, vector normal y vector unitario. | |sinopsis=Tipos de vectores: vector director, vector opuesto, vector normal y vector unitario. | ||
| |url1=https://youtu.be/7HkQ-Q0dS0w?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | |url1=https://youtu.be/7HkQ-Q0dS0w?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| - | }} | ||
| - | {{Video_enlace_pildoras | ||
| - | |titulo1=Vector entre dos puntos | ||
| - | |duracion=8'28" | ||
| - | |sinopsis=Cómo calcular un vector entre dos puntos | ||
| - | |url1=https://youtu.be/r1KOayxAUq8?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| }} | }} | ||
| {{Video_enlace_pildoras | {{Video_enlace_pildoras | ||
| Línea 58: | Línea 52: | ||
| |sinopsis=Suma y resta de vectores | |sinopsis=Suma y resta de vectores | ||
| |url1=https://youtu.be/OkiIB2fU_JM?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | |url1=https://youtu.be/OkiIB2fU_JM?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | }} | ||
| + | ==Vectores y puntos== | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Vector entre dos puntos | ||
| + | |duracion=8'28" | ||
| + | |sinopsis=Cómo calcular un vector entre dos puntos | ||
| + | |url1=https://youtu.be/r1KOayxAUq8?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| }} | }} | ||
| {{Video_enlace_pildoras | {{Video_enlace_pildoras | ||
| Línea 66: | Línea 67: | ||
| Advertencia: En este video cuando dice que suma un punto {{sube|porcentaje=+20%|contenido=<math>P\;</math>}} con un vector {{sube|porcentaje=+50%|contenido=<math>\overrightarrow{AB}</math>}}, en realidad lo que está haciendo es sumar dos vectores: {{sube|porcentaje=+50%|contenido=<math>\overrightarrow{OP}</math>}} y {{sube|porcentaje=+50%|contenido=<math>\overrightarrow{AB}</math>}}, donde {{sube|porcentaje=+20%|contenido=<math>O\;</math> es el origen de coordenadas}}. | Advertencia: En este video cuando dice que suma un punto {{sube|porcentaje=+20%|contenido=<math>P\;</math>}} con un vector {{sube|porcentaje=+50%|contenido=<math>\overrightarrow{AB}</math>}}, en realidad lo que está haciendo es sumar dos vectores: {{sube|porcentaje=+50%|contenido=<math>\overrightarrow{OP}</math>}} y {{sube|porcentaje=+50%|contenido=<math>\overrightarrow{AB}</math>}}, donde {{sube|porcentaje=+20%|contenido=<math>O\;</math> es el origen de coordenadas}}. | ||
| |url1=https://youtu.be/YXj0nGT0Ck4?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | |url1=https://youtu.be/YXj0nGT0Ck4?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tres puntos alineados | ||
| + | |duracion=7'25" | ||
| + | |sinopsis=Cómo averiguar si tres puntos están alineados | ||
| + | |url1=https://youtu.be/SSkwa9oS0dY?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 14:47 14 sep 2019
Menú:
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Sistema de coordenadas cartesianas
Ejes y puntos (12'04") Sinopsis:Geometría analítica. Sistema de ejes coordenados. Coordenadas de puntos en el plano.
Vectores en el plano
Qué es un vector (6'54") Sinopsis:Qué es un vector.
Coordenadas y pendiente de un vector (7'06") Sinopsis:Coordenadas y pendiente de un vector.
Módulo de un vector (6'16") Sinopsis:Módulo de un vector.
Argumento de un vector (9'46") Sinopsis:Argumento de un vector.
Tipos de vectores (13'26") Sinopsis:Tipos de vectores: vector director, vector opuesto, vector normal y vector unitario.
Suma y resta de vectores (11'23") Sinopsis:Suma y resta de vectores
Vectores y puntos
Vector entre dos puntos (8'28") Sinopsis:Cómo calcular un vector entre dos puntos
Traslación de un punto mediante un vector (9'47") Sinopsis:Traslación de un punto mediante un vector.
Advertencia: En este video cuando dice que suma un punto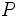 
con un vector 
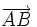, en realidad lo que está haciendo es sumar dos vectores: 
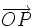y 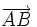, donde 
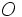es el origen de coordenadas.
Tres puntos alineados (7'25") Sinopsis:Cómo averiguar si tres puntos están alineados
