Integral definida (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:49 15 sep 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:57 15 sep 2019 Coordinador (Discusión | contribuciones) (→Integral definida) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| |duracion=12'47" | |duracion=12'47" | ||
| |url1=https://youtu.be/VIIXxanNF3o?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | |url1=https://youtu.be/VIIXxanNF3o?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| - | |sinopsis=Qué es la integral definida. Regla de Barrow. Ejemplos con Geogebra. | + | |sinopsis=La integral definida: Área entre una función y el eje X. Regla de Barrow. Ejemplos con Geogebra. |
| }} | }} | ||
| + | ==Área entre una función y el eje X== | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Área entre una función y el eje X | ||
| + | |duracion=12'09" | ||
| + | |url1=https://youtu.be/A4kctby_Ki4?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis=A la hora de calcular el área hay que tener cuidado con el "signo" de ésta. Ejemplos. | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplo 1 | ||
| + | |duracion=16'01" | ||
| + | |url1=https://youtu.be/04PhtWZwWC0?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis= | ||
| + | #Calcula el área entre la función <math>y=2x-3\;</math>, el eje X y las rectas x=-1 y x=2. | ||
| + | #Calcula el área entre la función <math>y=x^3-x^2-6x\;</math> y el eje X. | ||
| + | #Calcula el área entre la función <math>y=ln\,x</math>, el eje X y las rectas x=1 y x=4. | ||
| + | }} | ||
| + | |||
| ==Ejercicios== | ==Ejercicios== | ||
| {{Videotutoriales|titulo=Integrales definidas inmediatas|enunciado= | {{Videotutoriales|titulo=Integrales definidas inmediatas|enunciado= | ||
Revisión de 16:57 15 sep 2019
Tabla de contenidos |
Introducción
Qué es integrar. Una aproximación al concepto de integración.
Integral definida
La integral definida: Área entre una función y el eje X. Regla de Barrow. Ejemplos con Geogebra.
Área entre una función y el eje X
A la hora de calcular el área hay que tener cuidado con el "signo" de ésta. Ejemplos.
- Calcula el área entre la función
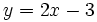 , el eje X y las rectas x=-1 y x=2.
, el eje X y las rectas x=-1 y x=2.
- Calcula el área entre la función
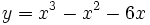 y el eje X.
y el eje X.
- Calcula el área entre la función
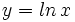 , el eje X y las rectas x=1 y x=4.
, el eje X y las rectas x=1 y x=4.
Ejercicios
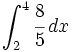
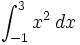
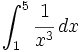
![\int_{-3}^{-1} \sqrt[3]{x^2} \, dx](/wikipedia/images/math/3/e/f/3ef78dfc1afd5490f8140c018cd83d2a.png)
![\int_{1}^{4} \sqrt[3]{27t} \, dt](/wikipedia/images/math/6/4/a/64af5171106055e85891eaee3fbc4713.png)
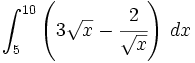
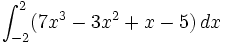
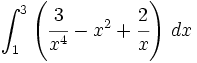
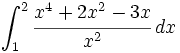
Calcula 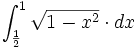 haciendo el cambio de variable
haciendo el cambio de variable 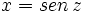 .
.
Calcula 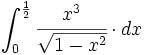 .
.
Calcula No se pudo entender (error de sintaxis): \int_{0}^{1} \cfrac{x^3+3x^2-3x}{x^2+3x+2}} \cdot dx .

