Plantilla:Límite de cociente de funciones polinómicas
De Wikipedia
| Revisión de 16:24 1 abr 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 53: | Línea 53: | ||
| |url1=https://youtu.be/WCmsYJfUTM8 | |url1=https://youtu.be/WCmsYJfUTM8 | ||
| }} | }} | ||
| - | }} | + | ---- |
| - | {{Videotutoriales | + | '''Límite de cociente de funciones polinómicas (Tipo a/0)''' |
| - | |titulo=Ejercicios: ''Límite de cociente de funciones polinómicas (Tipo a/0)'' | + | |
| - | |enunciado= | + | |
| - | + | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 85: | Línea 82: | ||
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/02-limites-de-funciones-2/0801-dos-ejercicios-7 | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/02-limites-de-funciones-2/0801-dos-ejercicios-7 | ||
| }} | }} | ||
| + | ---- | ||
| + | '''Límite de cociente de funciones polinómicas (Tipo 0/0)''' | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Videotutoriales | ||
| - | |titulo=Ejercicios: ''Límite de cociente de funciones polinómicas (Tipo 0/0)'' | ||
| - | |enunciado= | ||
| {{Tabla50|celda1= | {{Tabla50|celda1= | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
Revisión actual
Procedimiento
Sea 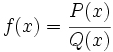 , con
, con  y
y  dos polinomios en x.
dos polinomios en x.
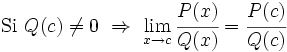
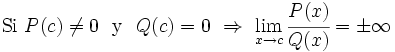 . En este caso será necesario estudiar los límites laterales para determinar el signo del infinito por cada lado. Podemos hacer uso de la calculadora.
. En este caso será necesario estudiar los límites laterales para determinar el signo del infinito por cada lado. Podemos hacer uso de la calculadora.
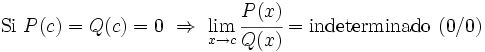 . Para resolver la indeterminación simplificaremos la fracción, ya que al anularese los dos polinomios deberán tener factores comunes. Una vez simplificada volveremos a calcular el límite, pudiendo darse cualquiera de las tres situaciones que acabamos de ver, repitiendo el proceso hasta que estemos en los caso 1 ó 2 y quede calculado el límite.
. Para resolver la indeterminación simplificaremos la fracción, ya que al anularese los dos polinomios deberán tener factores comunes. Una vez simplificada volveremos a calcular el límite, pudiendo darse cualquiera de las tres situaciones que acabamos de ver, repitiendo el proceso hasta que estemos en los caso 1 ó 2 y quede calculado el límite.
Ejemplo: Límite de una función cociente de polinomios
Calcula el valor de los siguientes límites y haz un esbozo gráfico del resultado:
- a)
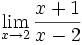 b)
b) 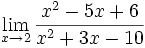
a) Estamos en el el segundo caso y tendremos que estudiar los límites laterales:
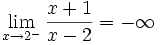 . Usando la calculadora, dando a x valores próximos a 2 por la izquierda: 1.99, 1.999,...
. Usando la calculadora, dando a x valores próximos a 2 por la izquierda: 1.99, 1.999,...
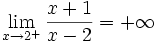 . Usando la calculadora, dando a x valores próximos a 2 por la derecha: 2.01, 2.001,...
. Usando la calculadora, dando a x valores próximos a 2 por la derecha: 2.01, 2.001,...
b) Estamos en el caso 3 porque numerador y el denominador se anulan en x=2 (indeterminación del tipo 0/0). Debemos simplificar la fracción:
- Ahora estamos en el caso 1:
Para ver el comportamiento gráfico usa la siguiente escena de Geogebra:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Estudio de la continuidad de una función dada por su gráfica.
Ejemplos de cada uno de los tres casos de límites de cociente de funciones polinómicas.
- a)
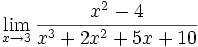
- b)
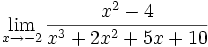
- c)
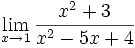
Límite de cociente de funciones polinómicas (Tipo a/0)
3 ejemplos de límites del tipo a/0:
- a)
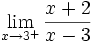
- b)
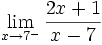
- c)
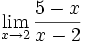
Límite del tipo a/0:
2 ejemplos de límites del tipo a/0:
- a)
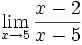
- b)
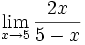
Límite de cociente de funciones polinómicas (Tipo 0/0)
Límite del tipo 0/0: 2 ejercicios de límites del tipo 0/0:
Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: | Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: Límite del tipo 0/0: |
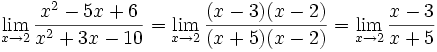
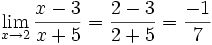
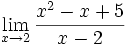
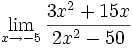
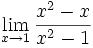
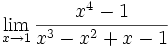
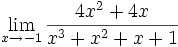
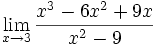
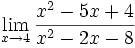
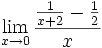
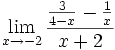
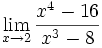
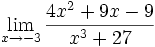
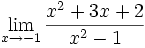
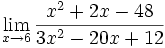
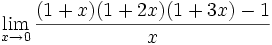
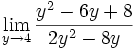
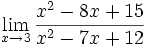
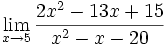
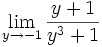
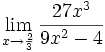
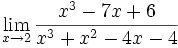
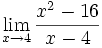
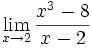
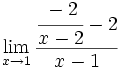
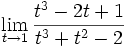
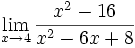
![\lim_{x \to 3} \frac{x^2-9}{\sqrt[3]{x}-\sqrt[3]{3}}](/wikipedia/images/math/5/0/f/50f7717bab4b7aff16f607347c53a91c.png)
![\lim_{x \to -1} \frac{x^3+1}{\sqrt[3]{x}+1}](/wikipedia/images/math/6/e/2/6e2b0bd19c53aea5c20f6feee8d5c091.png)
![\lim_{x \to \frac{2}{3}} \frac{\sqrt[3]{9x^2+4}-2}{3x-2}](/wikipedia/images/math/a/3/1/a31ec1f5b9b0fa43c24dd3b388bb6d40.png)

