Circunferencia (1º ESO)
De Wikipedia
| Revisión de 17:03 5 abr 2020 Coordinador (Discusión | contribuciones) (→Posiciones relativas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Posiciones relativas) |
||
| Línea 111: | Línea 111: | ||
| |sinopsis=Posiciones relativas de recta y circunferencia respecto de una circunferencia. | |sinopsis=Posiciones relativas de recta y circunferencia respecto de una circunferencia. | ||
| |url1=https://youtu.be/X69DFgok0J4 | |url1=https://youtu.be/X69DFgok0J4 | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=7'52" | ||
| + | |sinopsis=Posiciones relativas de un punto, recta y circunferencia respecto de una circunferencia. | ||
| + | |url1=https://youtu.be/XNGWQDJ4p5Q | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
La circunferencia y el círculo
- Una circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.
- El círculo es la figura geométrica delimitada por la circunferencia.
Trazado de la circunferencia Descripción: En esta escena podrás ver como se dibuja una circunferencia.
Circunferencia y círculo Descripción: Actividades sobre la circunferencia y el círculo
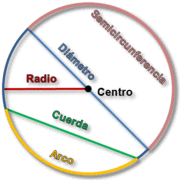
Elementos de la circunferencia
|  |
Tutorial 1 (10'10") Sinopsis:- Definición de circunferencia.
- Elementos de una circunferencia.
Tutorial 2 (10'02") Sinopsis:- La circunferencia y el círculo.
- Elementos de la circunferencia.
Tutorial 2b (3'06") Sinopsis:Las figuras circulares: semicírculo, sector circular, segmento circular y corona circular.
Tutorial 3 (1'57") Sinopsis: La circunferencia y el círculo. Elementos de la circunferencia. Figuras circulares.
Tutorial 4 (5'46") Sinopsis:La circunferencia y el círculo. Elementos de la circunferencia. Figuras circulares.
Presentación Descripción: La circunferencia y el círculo. Elementos.
Actividad 1a Descripción: Definición de circunferencia.
Actividad 1b Descripción: Escena en la que podrás ver los elementos más notables de una circunferencia. También podrás practicar con unas actividades.
Actividad 2 Descripción: Circunferencia, radio y diámetro.
Autoevaluación 1 Descripción: Radio y diámetro.
Autoevaluación 2 Descripción: Test sobre la circunferencia y el círculo.
Posiciones relativas
El siguiente video resume todo lo que vamos a ver en este apartado sobre las posiciones relativas de un punto, recta y circunferencia respecto de una circunferencia.
Tutorial 1 (15'49") Sinopsis:Posiciones relativas de un punto, recta y circunferencia respecto de una circunferencia.
Tutorial 2 (3'30") Sinopsis:Posiciones relativas de recta y circunferencia respecto de una circunferencia.
Tutorial 3 (7'52") Sinopsis:Posiciones relativas de un punto, recta y circunferencia respecto de una circunferencia.
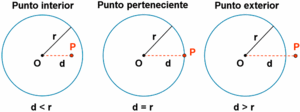
Posición relativa de un punto y una circunferencia
Un punto puede estar situado:
|  |
Posición relativa punto-circunferencia Descripción: Escena en la que podrás ver las distintas posiciones que puede tener un punto con respecto a una circunferencia.
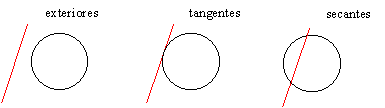
Posición relativa de una recta y una circunferencia
Una recta y una circunferencia pueden ser:
|  |
Posición relativa de una recta y una circunferencia Descripción: En esta escena podrás ver las distintas posiciones relativas de una recta y una circunferencia.
Posición relativa recta-circunferencia Descripción: Escena en la que podrás ver las distintas posiciones que puede tener una recta con respecto a una circunferencia.
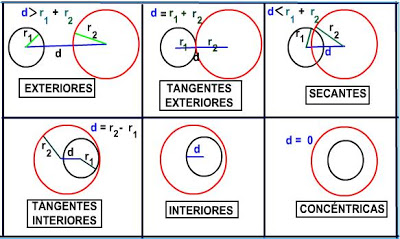
Posición relativa de dos circunferencias
Dos circunferencias pueden ser:
- Exteriores, si no tienen puntos comunes.
- Cumplen que la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio.
- Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. :Cumplen que la distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio.
- Secantes, si se cortan en dos puntos distintos.
- Cumplen que la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos.
- Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto.
- Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra.
- Cumplen que la distancia que hay entre sus centros es igual a la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores excéntricas, si no tienen ningún punto común.
- Cumplen que la distancia entre sus centros es mayor que 0 y menor que la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores concéntricas, si tienen el mismo centro y distinto radio.
- Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra.
- Coincidentes, si tienen el mismo centro y el mismo radio.
- En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes.
Posiciones relativas de dos circunferencias (16'40") Sinopsis:Posiciones relativas de dos circunferencias. Propiedades.
Posición relativa de dos circunferencias Descripción: Escena en la que podrás ver las distintas posiciones relativas entre dos circunferencias. También podrás practicar con unas actividades.
Actividades
Posiciones relativas Descripción: - Posiciones relativas de recta y circunferencia.
- Posiciones relativas de dos circunferencias.
Trazado de tangentes a una circunferencia Descripción: Actividades en las que podrás aprender a trazar tangentes a una circunferencia pasando un punto de la misma o por un punto exterior a ella.
