Parámetros estadísticos (1º ESO)
De Wikipedia
| Revisión de 08:57 20 abr 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:01 20 abr 2020 Coordinador (Discusión | contribuciones) (→Mediana) Ir a siguiente diferencia → |
||
| Línea 110: | Línea 110: | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Mediana|enunciado= | {{Videotutoriales|titulo=Mediana|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=8'49" | ||
| + | |sinopsis=Mediana con datos no agrupados. Ejemplos. | ||
| + | |url1=https://youtu.be/vq_f69udZfc?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=9'41" | ||
| + | |sinopsis=Mediana con datos agrupados. Ejemplos. | ||
| + | |url1=https://youtu.be/AfVWzR2k4EY?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| + | }} | ||
| {{Video_enlace_tutomate | {{Video_enlace_tutomate | ||
| |titulo1=Ejemplo 1 | |titulo1=Ejemplo 1 | ||
Revisión de 09:01 20 abr 2020
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Parámetros estadísticos
Después de haber representado los datos gráficamente, ahora llega el momento de hacer un estudio de los mismos. Existen una serie de datos que llamaremos parámetros estadísticos que nos sirven para representar a toda la población o que nos dan a información útil sobre la misma.
Parámetros estadísticos: Son datos que resumen el estudio realizado en la población. Pueden ser de dos tipos:
- Parámetros de centralización. Son datos que representan de forma global a toda la población. Entre ellos tenemos la media aritmética, la moda y la mediana.
- Parámetros de dispersión. Son datos que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización. Entre ellos están el recorrido, la desviación media, la varianza y la desviación típica.
Parámetros de centralización
Introducción a los parámetros de centralización.
Moda
- Se define la moda como el valor de la variable que más se repite, es el decir, aquél que tiene mayor frecuencia absoluta. Se representa por Mo.
- Si hay dos o varias puntuaciones con la misma frecuencia máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
Actividades en la que podrás aprender a calcular la moda de una distribución estadística.
Actividades en la que podrás aprender a calcular la moda de una distribución estadística.
Ejemplos con los que podrás aprender a calcular la moda de una distribución estadística.
Calcula en tu cuaderno la moda para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
a) Modifica las frecuencias y observa como puede variar el valor de la moda.
b) ¿Puede una distribución estadística tener más de una moda? ¿Pueden ser todos los valores de la variable?
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la moda de una distribución estadística.
Ejercicios de autoevaluación sobre el cálculo de la moda.
Cálculo de la moda.
Media
Se define la media como la suma de todos los datos dividida por el número de datos. Se representa por 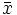 .
.
Para calcular la media hacemos:
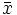 =
= 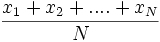 .
.
Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula:
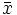 =
= 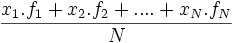
Media. Ejemplos.
Cálculo de la media para datos no agrupados.
Actividades en la que podrás aprender a calcular la media de una distribución estadística.
Actividades en la que podrás aprender a calcular la media de una distribución estadística.
Ejemplos de cálculo de medias de un conjunto de pocos datos.
Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la media.
- ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.
- ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.
Actividades para que practiques el cálculo de medias de un conjunto de pocos datos.
Mediana
Si ordenamos todos los valores de la variable de menor a mayor, se define la mediana como el valor de la variable que está en el centro. Se representa por Me.
Cálculo de la mediana
Para calcular la mediana es necesario que los datos estén ordenados de menor a mayor. Si hay un número impar de datos observados, habrá un sólo valor central, mientras que si hay un número par de datos habrá que hallar la media de los dos valores centrales. En el caso de datos agrupados puntualmente deberemos guiarnos con las frecuencias acumuladas.
Mediana con datos no agrupados. Ejemplos.
Mediana con datos agrupados. Ejemplos.
Cálculo de la mediana para datos no agrupados. Ejemplos.
Cálculo de la mediana para datos no agrupados. Ejemplos.
Datos no agrupados:
Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con los datos no agrupados.
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística.
Ejercicios de autoevaluación sobre la mediana.
Datos agrupados puntualmente:
Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con muchos datos en tabla de frecuencias.
Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la mediana.
- ¿Cuál es el valor menor que puede tomar? ¿Y el mayor?
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística con muchos datos en tabla de frecuencias.
Parámetros de dispersión
Introducción a los parámetros de dispersión.
Rango o recorrido
Se define el rango o recorrido como la diferencia entre el mayor y el menor de los valores de la variable. Se representa por R.
Rango o recorrido. Ejemplos.
Rango o recorrido. Ejemplos.
Ejemplos con los que podrás aprender a calcular el rango de una distribución estadística.
Actividades para comprobar lo que has aprendido sobre el cálculo del rango de una distribución estadística.
Desviación media
- La diferencia entre cada dato y la media aritmética del grupo se llaman desviaciones respecto a la media.
- Desviación media de un conjunto de datos es la media aritmética de los valores absolutos de las desviaciones respecto a la media. Nos indica el grado de dispersón (alejamiento) de los datos respecto a su media.
Desviación media. Ejemplos.
Desviación media con más datos. Ejemplos.
Desviaciones respecto a la media. Ejemplos.
Desviación media. Ejemplos.
Ejercicios de autoevaluación sobre el cálculo de la desviación media.
Ejercicios de autoevaluación sobre la desviación media.
Actividades en la que podrás aprender a calcular el rango y la deviación media de una distribución estadística.
Actividades y videotutoriales
Cálculo de la media, la moda y la mediana.
Cálculo de la media, la moda, la mediana y el rango.
Cálculo de la media, la moda y la mediana.
Cálculo de la media, la moda y la mediana con una hoja de cálculo.
Actividades en la que podrás aprender a calcular el rango y la mediana de una distribución estadística.
Actividades en la que podrás aprender a interpretar y aplicar los parámetros estadísticos.

