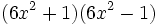Plantilla:Videos: identidades notables
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:54 28 sep 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 57: | Línea 57: | ||
| |sinopsis=Como se desarrollan un binomio al cuadrado y una suma por diferencia. | |sinopsis=Como se desarrollan un binomio al cuadrado y una suma por diferencia. | ||
| |url1=https://www.youtube.com/watch?v=mTkBiySoIzQ&list=PLw7Z_p6_h3oxSaTeel6R_pQaMSalig8UR | |url1=https://www.youtube.com/watch?v=mTkBiySoIzQ&list=PLw7Z_p6_h3oxSaTeel6R_pQaMSalig8UR | ||
| + | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 5 | ||
| + | |duracion=25'26" | ||
| + | |sinopsis=Explicación de las igualdades o identidades notables y ejemplos resueltos. | ||
| + | |url1=https://youtu.be/r15dHPFYNKo | ||
| }} | }} | ||
| ---- | ---- | ||
Revisión actual
Productos notables. Ejemplos.
Las tres identidades notables.
La identidad notable cuadrado de una suma. Ejemplos.
La identidad notable cuadrado de una diferencia. Ejemplos.
La identidad notable suma por diferencia. Ejemplos.
- Fórmulas del cuadrado de una suma y de una diferencia.
- Ejemplos::
- a)

- b)
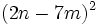
- Fórmula de la suma por diferencia.
- Ejemplos:
- a)
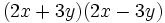
- b)
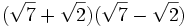
- c)
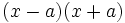
Como se desarrollan un binomio al cuadrado y una suma por diferencia.
Explicación de las igualdades o identidades notables y ejemplos resueltos.
Desarrolla:
- a)
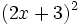
- b)
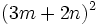
- c)
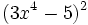
- d)
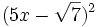
Desarrolla:
- a)
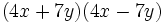
- b)
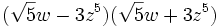
- c)

Desarrolla: 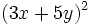
Desarrolla: 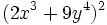
Desarrolla: 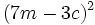
Desarrolla: 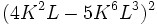
Desarrolla: 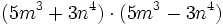
Desarrolla:
a) 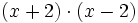
b) 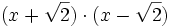
c) 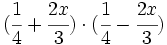
d) 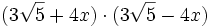
e) 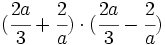
Desarrolla los siguientes productos notables:
- 2a)
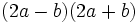
- 2b)
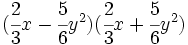
- 2c)
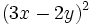
- 2d)
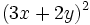
- 2e)
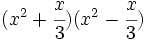
Desarrolla los siguientes productos notables:
- 4a)
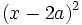
- 4b)
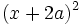
- 4c)
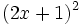
- 4d)
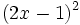
Desarrolla los siguientes productos notables:
- 5a)
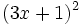
- 5b)
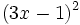
- 5c)
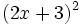
- 5d)
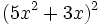
- 5e)
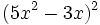
- 5f)
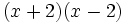
- 5g)
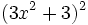
- 5h)
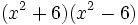
- 5i)
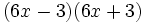
- 5j)
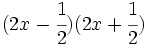
- 5k)
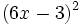
- 5l)
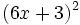
Calcula: 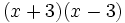
Calcula: 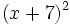
Calcula: 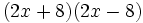
Calcula: 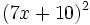
Halla el área de un cuadrado cuyo lado mide 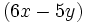 .
.
Calcula:
- a)
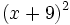
- b)
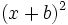
- c)
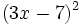
- d)
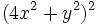
- e)
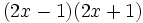
- f)
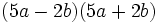
Calcula:
- a)
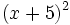
- b)
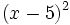
- c)
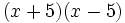
- d)
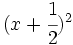
- e)
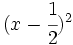
- f)
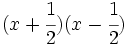
- g)
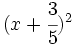
- h)
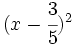
- i)
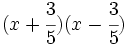
- j)
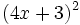
- k)
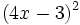
- l)
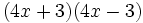
- m)
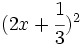
- n)
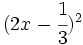
- o)
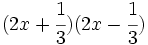
- p)
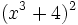
- q)
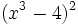
- r)
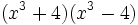
- s)
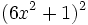
- t)
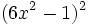
- u)