Vídeos de Matemáticas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 20:06 6 dic 2007 Juanmf (Discusión | contribuciones) (→UNIVERSO MATEMÁTICO) ← Ir a diferencia anterior |
Revisión de 20:09 6 dic 2007 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 19: | Línea 19: | ||
| {{Desplegable | {{Desplegable | ||
| |titulo=<font color="#0000FF"> | |titulo=<font color="#0000FF"> | ||
| - | + | [http://maralboran.org/web_ma/videos/fermat/fermat.htm Fermat, el margen más famoso de la historia (22')] - [ (acceso por red TIC)] | |
| </font> <font color="#000000"></font> | </font> <font color="#000000"></font> | ||
| - | |contenido= | + | |contenido=A principios de siglo XVII un abogado, aficionado a las matemáticas va a lanzar una serie de retos, basados en los números más simples, los enteros, a toda la comunidad matemática. Es Pierre de Fermat. La inspiración para estos retos la encontró en un antiguo libro de matemáticas escrito allá por el siglo III, la Aritmética de Diofanto. En uno de sus márgenes Fermat va a escribir una frase que se convertirá en una de las más atractivas de la historia de las matemáticas. Su famoso último teorema: |
| + | |||
| + | “No existen soluciones enteras para la ecuación <math>x^n + y^n = z^n \,cuando n> 2</math>” | ||
| + | |||
| + | Fermat afirma que había encontrado la demostración pero por desgracia no le cabe el margen. Una desgracia que ha traído en jaque a los mejores matemáticos durante más de 350 años. Haremos un recorrido histórico por los intentos de demostrar este teorema a lo largo de tres siglos y presentaremos a Wiles, un matemático inglés que en 1994 pasó a la historia… Por fin alguien había conseguido demostrar el “ultimo teorema de Fermat” | ||
| + | |||
| + | |||
| }} | }} | ||
Revisión de 20:09 6 dic 2007
UNIVERSO MATEMÁTICO
Pitágoras: mucho más que un teorema(25') - [ (acceso por red TIC)]
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Perolas Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.
Si las matemáticas tienen algún número emblemático ese es PI: 3,141592…La figura de Ramanujan, un joven indio sin formación universitaria está intimamente ligada al número pi. A principio de siglo descubrió nuevas series infinitas para obtener valores aproximados de pi. Lasmismas que utilizan los grandes ordenadores para obtener millones de cifras de este familiar y extraño número.Pero el verdadero padre de pi es un matemático griego de hace 2.300 años, Arquímedes. Él descubrió la famosa fórmula del área del círculo. Y también el volumen y el área de la esfera. De paso invento el primer método para obtener valores aproximados de pi aproximando el círculo mediante polígonos de un número creciente de lados.Pero pi no sólo aparece en matemáticas cuando se habla de círculos o esferas, su presencia en relaciones numéricas, en el cálculo de probabilidades y hasta en estudiosestadísticos la confieren una omnipresencia casi mágica.
Números y cifras, un viaje en el tiempo (24') - [ (acceso por red TIC)]
Con la llegada del euro volverán los céntimos y unos viejos conocidos van a adquirir un protagonismo social que no tenían desde hace mucho tiempo: los números decimales. Unos números que, a pesar de la creencia popular de que existen desde los comienzos de las matemáticas, sólo llevan entre nosotros cuatro siglos. Y es que la historia de los números es más compleja de lo que sospechamos. A lo largo del programa haremos una excursión por el tiempo para descubrir la historia de las cifras. Descubriremos las cifras y la forma de utilizarlas de babilonios, egipcios, griegos y romanos hasta llegar hasta nuestras populares 10 cifras: 1, 2, 3, 4, 5… Pero incluso estas cifras heredadas de los árabes no siempre han sido la herramienta habitula para calcular. Conoceremos las aventuras de estos símbolos desde su nacimiento hasta nuestros días, en que sin duda son los símbolos más universalmente utilizados.
Fermat, el margen más famoso de la historia (22') - [ (acceso por red TIC)]
A principios de siglo XVII un abogado, aficionado a las matemáticas va a lanzar una serie de retos, basados en los números más simples, los enteros, a toda la comunidad matemática. Es Pierre de Fermat. La inspiración para estos retos la encontró en un antiguo libro de matemáticas escrito allá por el siglo III, la Aritmética de Diofanto. En uno de sus márgenes Fermat va a escribir una frase que se convertirá en una de las más atractivas de la historia de las matemáticas. Su famoso último teorema:
“No existen soluciones enteras para la ecuación 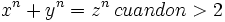 ”
”
Números
- El número e (13') - (acceso por red TIC)
- El número pi (25') - (acceso por red TIC)
- La divina proporción: el número phi (6') - (acceso por red TIC)
- Las cifras un viaje en el tiempo (24') - [ (acceso por red TIC)]
- Nº naturales, nº primos (17') - [ (acceso por red TIC)]
Funciones
- Derivadas (26') - [ (acceso por red TIC)]
Matemáticos
- Pitágoras (25') - [ (acceso por red TIC)]
- Newton y Leibnitz (19') - [ (acceso por red TIC)]
- Euler (22') - [ (acceso por red TIC)]
- Fermat (22') - [ (acceso por red TIC)]
- Gauss (22') - [ (acceso por red TIC)]
- Mujeres matemáticas (21') - (acceso por red TIC)

