Números Reales (4ºESO Académicas)
De Wikipedia
| Revisión de 11:28 9 jul 2008 Juanmf (Discusión | contribuciones) (→La recta real) ← Ir a diferencia anterior |
Revisión de 11:31 9 jul 2008 Juanmf (Discusión | contribuciones) (→La recta real) Ir a siguiente diferencia → |
||
| Línea 31: | Línea 31: | ||
| ==La recta real== | ==La recta real== | ||
| - | La '''recta real''' es una representación geométrica del conjunto de los números reales. Tiene su origen en el cero, y se extiende en ambas direcciones, los positivos hacia la derecha y los negativos a la izquierda. Existe una correspondencia uno a uno entre cada punto de la recta y un número real. | + | La '''recta real''' es una representación geométrica del conjunto de los números reales. Tiene su origen en el cero, y se extiende en ambas direcciones, los positivos hacia la derecha y los negativos a la izquierda. Existe una correspondencia uno a uno entre cada punto de la recta y un número real, es decir,''' a cada punto de la recta le corresponde un número real y viceversa'''. |
| [[Image:Recta real.png|800px]] | [[Image:Recta real.png|800px]] | ||
Revisión de 11:31 9 jul 2008
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Conjuntos numéricos
El conjunto formado por los números racionales y los irracionales se llama conjunto de los números reales y se designa por  .
.
En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora:
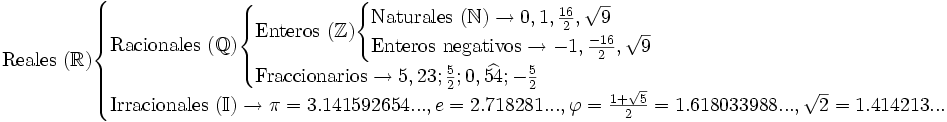
La recta real
La recta real es una representación geométrica del conjunto de los números reales. Tiene su origen en el cero, y se extiende en ambas direcciones, los positivos hacia la derecha y los negativos a la izquierda. Existe una correspondencia uno a uno entre cada punto de la recta y un número real, es decir, a cada punto de la recta le corresponde un número real y viceversa.

Esta recta numérica real, se construye como sigue: se elige de manera arbitraria un punto de una línea recta para que represente el cero o punto origen. Se elige un punto a una distancia adecuada a la derecha del origen para que represente al número 1. Esto establece la escala de la recta numérica.

