Medidas de Posición (4ºESO-B)
De Wikipedia
| Revisión de 18:35 9 jul 2008 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:38 9 jul 2008 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | {{Menú Matemáticas 4ESOB | ||
| + | |ir= | ||
| + | |ampliar= | ||
| + | |repasar= | ||
| + | |enlaces= | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| ==Medidas de posición== | ==Medidas de posición== | ||
| + | ===Mediana=== | ||
| + | <div style="background: white; border: 2px solid Gold;border-left: 4px solid Gold;border-bottom: 4px solid Gold; padding:.75em;"> | ||
| + | Si ordenamos todos los valores de la variable de menor a mayor, se define la '''mediana''' como el valor de la variable que está en el centro. Se representa por Me. Aquí tenemos que comprender que si hay un número impar de valores, habrá un sólo valor central; mientras que si hay un número par de valores habrá dos valores centrales. | ||
| + | </div> | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Mediana''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1'''. Variable discreta. | ||
| + | |actividad= Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/mediana_discreta_est.htm | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center>}} | ||
| + | }} | ||
| + | {{ejercicio | ||
| + | |titulo=Actividad: ''Mediana'' | ||
| + | |cuerpo= | ||
| + | '''Actividad 1:''' | ||
| + | :a) Modifica las frecuencias y observa como puede variar el valor de la mediana. | ||
| + | :b) ¿Cuál es el valor menor que puede tomar? ¿Y el mayor? | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| :'''Cuartiles'''. Son valores que dividen a la población en cuatro partes iguales. Los vamos a representar por <math>C_1, C_2 </math>y <math>C_3</math>. Entre cada dos de ellos estará el 25 % de los datos. Lógicamente el segundo cuartil coincidirá con la mediana. | :'''Cuartiles'''. Son valores que dividen a la población en cuatro partes iguales. Los vamos a representar por <math>C_1, C_2 </math>y <math>C_3</math>. Entre cada dos de ellos estará el 25 % de los datos. Lógicamente el segundo cuartil coincidirá con la mediana. | ||
Revisión de 18:38 9 jul 2008
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Medidas de posición
Mediana
Si ordenamos todos los valores de la variable de menor a mayor, se define la mediana como el valor de la variable que está en el centro. Se representa por Me. Aquí tenemos que comprender que si hay un número impar de valores, habrá un sólo valor central; mientras que si hay un número par de valores habrá dos valores centrales.
|
Actividad Interactiva: Mediana
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados. |
|
Actividad: Mediana Actividad 1:
|
- Cuartiles. Son valores que dividen a la población en cuatro partes iguales. Los vamos a representar por C1,C2y C3. Entre cada dos de ellos estará el 25 % de los datos. Lógicamente el segundo cuartil coincidirá con la mediana.
- Deciles. Son valores que dividen a la población en diez partes iguales. Los representaremos por Dn. El quinto decil coincide también con la mediana.
- Percentiles. Son valores que dividen a la población en cien partes iguales. Los representamos por Pn. Evidentemente los percentiles 25, 50 y 75 coinciden con los cuartiles. Y los percentiles 10, 20 , ... , 90 coinciden con los deciles.
El cálculo de estos parámetros, tanto para variables discretas como para variables continuas, se hace de forma similar al cálculo de la mediana.
Si la variable es discreta, para calcular un percentil, calcularemos el porcentaje de datos que corresponde a dicho percentil, es decir para calcular el percentil de orden "p", calcularemos 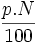 . Si este valor no coincide con ninguna de las frecuencias absolutas acumuladas, cogemos el primer valor de la variable cuya frecuencia absoluta acumulada supera este dato. Pero si este valor coincide con una frecuencia absoluta acumulada, el percentil buscado será la media aritmética entre el valor de la variable correspondiente y el siguiente.
. Si este valor no coincide con ninguna de las frecuencias absolutas acumuladas, cogemos el primer valor de la variable cuya frecuencia absoluta acumulada supera este dato. Pero si este valor coincide con una frecuencia absoluta acumulada, el percentil buscado será la media aritmética entre el valor de la variable correspondiente y el siguiente.
Si la variable es continua aplicamos la siguiente fórmula muy similar a la utilizada para el cálculo de la mediana:
|
|
|
Actividad Interactiva: Percentiles
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno los cuartiles primero y tercero para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que los tienes en tu cuaderno, calcúlalos con la escena y compara los resultados.
Actividad 2. Variable continua.
Actividad: Calcula en tu cuaderno los cuartiles primero y tercero para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes. Una vez que los tienes en tu cuaderno, calcúlalos con la escena y compara los resultados. |
|
Actividad: Percentiles Actividad 1: Modifica las frecuencias y calcula varios percentiles. |