Algunos límites importantes (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Suma de los términos de una progresión geométrica
Límite de la suma de n primeros términos de una progresión geométrica
Sea  una progresión geométrica de razón
una progresión geométrica de razón  y sea
y sea 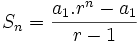 la suma de sus n primeros términos
la suma de sus n primeros términos
- Si
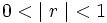 , entonces el límite de
, entonces el límite de 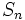 existe y vale:
existe y vale:
- Si
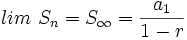
- Si
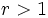 , entonces el límite de
, entonces el límite de 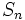 es
es 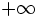 :
:
- Si
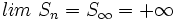
- Si
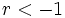 , entonces el límite de
, entonces el límite de 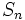 no existe.
no existe.
- Si
Demostración:
El número e
El número áureo, 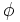
La sucesión de Fibonacci y el número áureo
Si a partir de la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...), construimos, por recurrencia, la sucesión 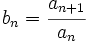 , se cumple que:
, se cumple que:
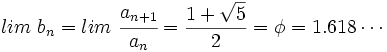 (número áureo)
(número áureo)Demostración:
Lo siguiente no es una demostración, sino una comprobación:
En efecto, si en la sucesión de Fibonacci
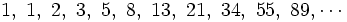
dividimos cada término entre el anterior, tenemos:
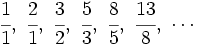
que expresada con decimales nos da:
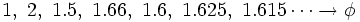
Video: La divina proporción. El número Phi. (6´)
Sinopsis:
Documental sobre la historia del número áureo, Phi
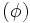 y la divina proporción.
y la divina proporción.Web: [Phi, el número de oro Phi, el número de oro]
Descripción:
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.

