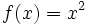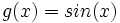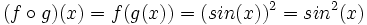Composición de funciones (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Función compuesta
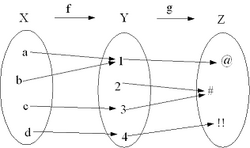
La función compuesta es una función formada por la aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. Formalmente:
Dadas dos funciones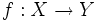 
y 
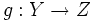, donde la imagen de 
está contenida en el dominio de definición de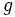 
, se define la función compuesta 
como 
, para todos los elementos 
de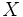 
.
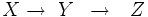
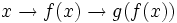
A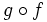 
se le llama composición de f y g. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
Ejemplo
Sean las funciones:
La función compuesta de g y de f que expresamos:
La interpretación de (f o g) aplicada a la variable x significa que primero tenemos que aplicar g a x, con lo que obtendríamos un valor de paso
y después aplicamos f a z para obtener
