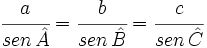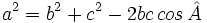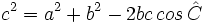Resolución de triángulos cualesquiera (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Teorema de los senos
Teorema de los senos
Demostración:
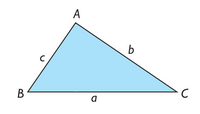
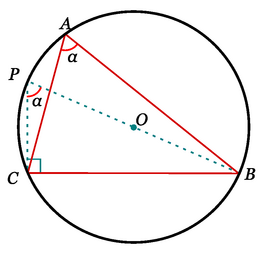
Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.
Ahora, el triángulo PBC es recto, puesto que BP es un diámetro, y además los ángulos A y P son iguales, porque ambos son ángulos inscritos que abarcan el mismo segmento BC. Por la definición de seno, se tiene
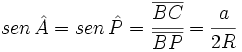
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
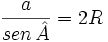
Teorema del coseno
Teorema del coseno
Demostración: