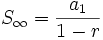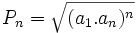Plantilla:Progresiones geométricas
De Wikipedia
Tabla de contenidos |
Progresiones geométricas
Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija,  , que llamaremos razón
, que llamaremos razón
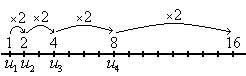
Por ejemplo:
es una progresión geométrica de razón r=2.
Término general de una progresión geométrica
Término general de una progresión geométrica
Sean 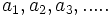 términos de una progresión geométrica de razón
términos de una progresión geométrica de razón  .
.
Entonces se cumple que:
|
|
En efecto, de forma intuitiva:
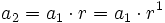

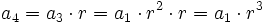
........................
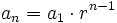
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
<center>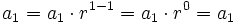
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n. Debemos comprobar que se cumple para el valor n+1.
Sustituimos n por n+1 en el lado derecho de la fórmula:
 [1]
[1]Por otro lado sabemos que 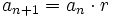 , y como hemos supuesto que la igualdad es cierta para el valor n,
, y como hemos supuesto que la igualdad es cierta para el valor n, 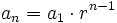 , tenemos que:
, tenemos que:
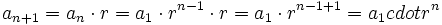
</center>
Suma de términos de una progresión geométrica
Suma de términos de una progresión geométrica
La suma de los n primeros términos de una progresión geométrica es:
|
|
Efectuamos la siguiente resta:
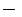
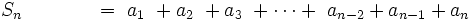
- ______________________________________________________________________________

por tanto:
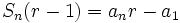
y despejando
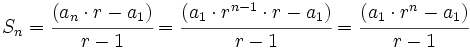
Suma de los infinitos términos de una progresión geométrica
La suma de todos los términos de una progresión geométrica en la que su razón verifica que 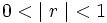 se obtiene así:
se obtiene así:
|
|
La siguiente demostración usa el concepto de límite que aún no conoceis. Lo podremos ver con detalle, más adelante en este tema, en un apartado titulado Algunos límites importantes.
Vamos a partir de la fórmula de la suma de los n primeros términos de una progresión geométrica y vamos a hacer que n tienda a infinito.
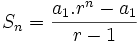
Como 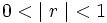 , cuando n tiende a infinito,
, cuando n tiende a infinito, 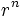 tiende a 0.
tiende a 0.
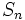 tiende a
tiende a 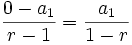 y a ese valor límite de
y a ese valor límite de 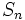 lo llamamos
lo llamamos 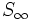 .
.
Producto de términos de una progresión geométrica
Producto de términos de una progresión geométrica
El producto de los n primeros términos de una progresión geométrica es:
|
|
Véase en el siguiente videotutorial:
Videotutorial