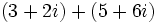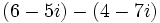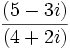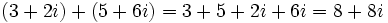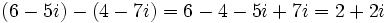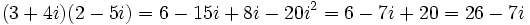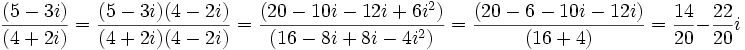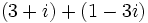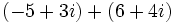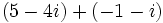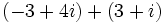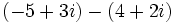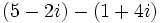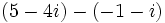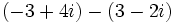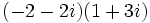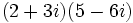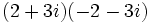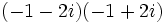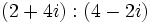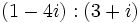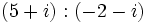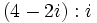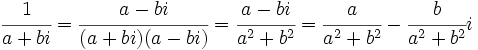Números complejos: Operaciones (1ºBach)

De Wikipedia

Revisión de fecha 18:10 30 sep 2014; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Geogebra Calculadoras

Operaciones con números complejos en forma binómica

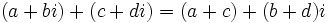
Suma: $\,(a + bi) + (c + di) = (a + c) + (b + d)i$
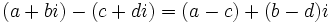
Resta: $\,(a + bi) - (c + di) = (a - c) + (b - d)i$
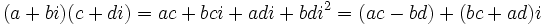
Multiplicación: $\,(a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i$
División: 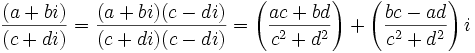$\,\frac{(a + bi)}{(c + di)} = \frac{(a + bi) (c - di)}{(c + di) (c - di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\,$ , siempre que 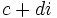$c+di\,$ no sea nulo.

Suma de números complejos (8´53") Sinopsis:

Videotutorial.

Producto de números complejos (11´26") Sinopsis:

Videotutorial.

Cociente de números complejos (7´45") Sinopsis:

Videotutorial.

Ejemplos: Operaciones con complejos en forma binómica

Efectúa las siguientes operaciones:

$\,(3 + 2i) + (5 + 6i)$
$\,(6 - 5i) - (4 - 7i)$
$\,(3 + 4i) (2 - 5i)$
$\,\frac{(5 - 3i)}{(4 + 2i)}$

Solución:

$\,(3 + 2i) + (5 + 6i)=3 + 5 + 2i + 6i=8 + 8i$
$\,(6 - 5i) - (4 - 7i)=6-4-5i+7i=2+2i$
$\,(3 + 4i) (2 - 5i)=6-15i+8i-20i^2=6-7i+20=26-7i$
$\,\frac{(5 - 3i)}{(4 + 2i)}=\frac{(5 - 3i)(4-2i)}{(4 + 2i)(4-2i)}=\frac{(20-10i-12i+6i^2)}{(16-8i+8i-4i^2)}=\frac{(20-6-10i-12i)}{(16+4)}=\frac{14}{20}-\frac{22}{20}i$

Ejercicios: Operaciones con números complejos en forma binómica

2 ejercicios (Suma) (5´55") Sinopsis:

Videotutorial.

3 ejercicios (Ecuaciones con soluciones complejas) (9´24") Sinopsis:

Videotutorial.

3 ejercicios (Producto) (9´19") Sinopsis:

Videotutorial.

3 ejercicios (Producto) (7´05") Sinopsis:

Videotutorial.

2 ejercicios (Cociente) (6´46") Sinopsis:

Videotutorial.

3 ejercicios (Cociente) (8´11") Sinopsis:

Videotutorial.

3 ejercicios (Cociente) (7´19") Sinopsis:

Videotutorial.

Actividad interactiva: Operaciones con números complejos

Suma: Efectúa las siguientes sumas de números complejos en tu cuaderno y haz una comprobación posterior en la escena:

$\,(3 + i) + (1 - 3i)$
$\,(-5 + 3i) + (6 + 4i)$
$\,(5 - 4i) + (-1 - i)$
$\,(-3 + 4i)+(3 + i)$

Actividad:

Utiliza el deslizador verde para comprobar cómo se obtiene la suma de dos complejos por el "método del paralelogramo"

Mueve los puntos azules para modificar los datos.

Click aquí si no se ve bien la escena

Resta: Efectúa las siguientes restas de números complejos en tu cuaderno y haz una comprobación posterior en la escena:

$\,(-5 + 3i) - (4 + 2i)$
$\,(5 -2i) -(1+ 4i)$
$\,(5 - 4i) - (-1 - i)$
$\,(-3 + 4i)-(3 - 2i)$

Actividad:

Utiliza el deslizador verde para comprobar cómo se obtiene la resta de dos complejos por el "método del paralelogramo"

Mueve los puntos azules para modificar los datos.

Click aquí si no se ve bien la escena

Otro modo de restar números complejos es sumar el opuesto: puedes comprobarlo en la siguiente figura:

Click aquí si no se ve bien la escena

Producto: Efectúa las siguientes multiplicaciones en tu cuaderno y haz una comprobación posterior en la escena:

$\,(-2 -2i) (1 + 3i)$
$\,(2 + 3i)(5-6i)$
$\,(2+3i)(-2-3i)$
$\,(-1-2i)(-1+2i)$

Actividad:

Utiliza el deslizador verde para comprobar cómo se obtiene el producto de dos complejos, a partir del triángulo construido a partir del primer número complejo, el origen de coordenadas y el punto (1,0).

Mueve los puntos azules para modificar los datos.

Click aquí si no se ve bien la escena

División: Efectúa las siguientes divisiones en tu cuaderno y compruébalas en la escena:

$\,(2+4i):(4-2i)$
$\,(1-4i):(3+i)$
$\,(5+i):(-2-i)$
$\,(4-2i):i$

Actividad:

Utiliza el deslizador verde para comprobar cómo se obtiene el cociente de dos complejos, a partir del triángulo construido a partir de los dos.

Mueve los puntos azules para modificar los datos.

Click aquí si no se ve bien la escena

Propiedades de las operaciones con números complejos

El 0 es el elemento neutro de la suma.
Todo número complejo, $a+bi\,$ , tiene un opuesto, $-a-bi\,$
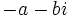
El 1 es el elemento neutro del producto.
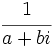Todo número complejo, $a+bi\,$ , distinto de 0, tiene inverso, $\cfrac{1}{a+bi}$ :