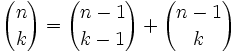Fórmula del binomio de Newton (1ºBach)
De Wikipedia
Binomio de Newton
Teorema: Fórmula del binomio de Newton
- El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula:
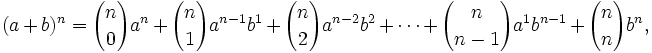
- que podemos expresar de forma abreviada de la siguiente manera:
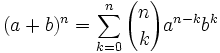
Atribuido a Newton, el teorema fue en realidad descubierto por primera vez por Al-Karaji alrededor del año 1000.
Coeficientes binomiales
Llamaremos coeficientes binomiales a los coeficientes | 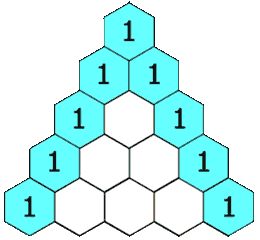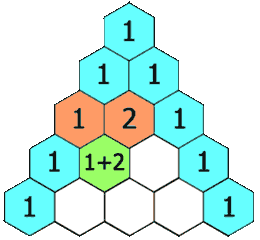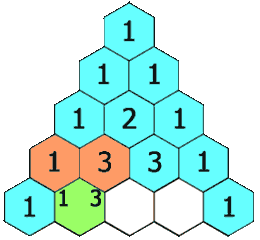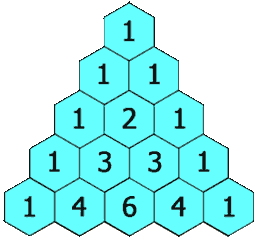
|
Triángulo de Pascal
El triángulo de Pascal es una representación de los coeficientes binomiales 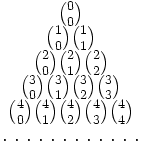 Cada casilla del triángulo se obtiene como suma de las dos que hay justo encima de ella. (Por la propiedad anterior) |
Es llamado así en honor al matemático francés Blaise Pascal, quien introdujo esta notación en 1654, en su Traité du triangle arithmétique. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta.
Propiedades
- Los coeficientes del desarrollo de (a+b)n se encuentran en la línea "n+1" del Triángulo de Pascal.
- El Triángulo de Pascal es simétrico.
- La suma de todos los valores de la fila "n" es igual a 2n.
- Esto es inmediato, por como está construido el Triángulo de Pascal.
- Esto es así porque
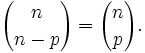 .
.
- Esto es debido a que, por el teorema del binomio, la expansión de la n-potencia de (1 + 1)n = 2n es
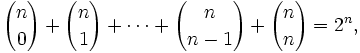
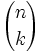 , de los términos del desarrollo del binomio de Newton.
, de los términos del desarrollo del binomio de Newton.