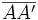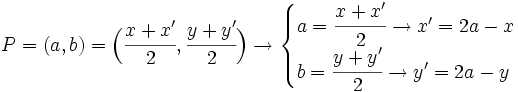Puntos y vectores el plano (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 188)
Sistema de referencia en el plano
Un sistema de referencia del plano consiste en una terna En este sistema de referencia, cada punto Si el vector Normalmente trabajaremos con un sistema de referencia ortonormal, que es aquel en el que la base es ortonormal. |
En esta escena podrás ver como se obtienen las coordenadas de un punto respecto de un sistema de referencia del plano a partir de su vector de posición.
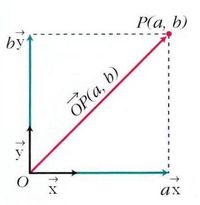
Coordenadas del vector que une dos puntos
Siendo P = (x0,y0) y Q = (x1,y1) puntos del plano, en este vídeo definimos el concepto de "vector fijo" asociado al par ordenado (P,Q). Visualizamos dicho vector fijo mediante una "flecha" que tiene origen en "P" y extremo en "Q". El vector fijo asociado al par (Q,P) se dice "opuesto" del asociado al par (P,Q). En términos matemáticos, el vector fijo asociado al par ordenado (P,Q) queda identificado mediante el par ordenado de números reales (x1 − x0,y1 − y0), que se obtiene al restar las coordenadas del punto "P" a las coordenadas del punto "Q". De dicho par (x1 − x0,y1 − y0) se dice que son las coordenadas del vector fijo.
Dados los puntos A(8,-2) y B(-3,-4), determina su módulo y su dirección (ángulo con los ejes).
Estudio del signo de las coordenadas de un vector 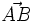 según la posición del origen A y el extremo B del vector.
según la posición del origen A y el extremo B del vector.
Siendo P = (x0,y0) y Q = (x1,y1) puntos del plano, las coordenadas del "vector fijo" asociado al par ordenado (P,Q) son 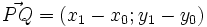 .
.
En este vídeo nos dan las coordenadas del vector fijo y las del punto "P" (punto "Q"), pidiéndonos que determinemos las coordenadas del punto "Q" (punto "P").
En esta escena podrás calcular las coordenadas del vector que une dos puntos del plano.
Vectores equipolentes
- Dos vectores fijos se dicen "equipolentes" si tienen el mismo módulo, dirección y sentido o, equivalentemente, si tienen las mismas coordenadas.
- Si el vector fijo asociado al par (M,N) es equipolente al vector fijo asociado al par (S,T), los segmentos MT y NS tienen el mismo punto medio, y si los puntos "M", "N", "S" y "T" nos están alineados, el polígono cuyos vértices son esos puntos es un paralelogramo.
- Se llama "vector libre" al CONJUNTO formado por un vector fijo y todos los equipolentes a él.
Conocidos 3 puntos del plano hallar un cuarto punto tal que forme con los otros tres un paralelogramo.
En esta escena podrás ver como vectores equipolentes tienen las mismas coordenadas.
Condición para que tres puntos estén alineados
Condición para que tres puntos estén alineados
Los puntos del plano 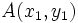 ,
, 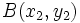 y
y 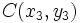 , están alineados si
, están alineados si 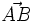 y
y 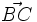 son vectores paralelos, es decir, si sus coordenadas son proporcionales:
son vectores paralelos, es decir, si sus coordenadas son proporcionales:
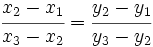
Los puntos del plano 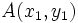 ,
, 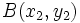 y
y 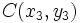 , están alineados si los vectores
, están alineados si los vectores 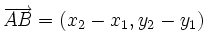 y
y 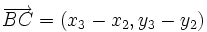 tienen la misma dirección.
tienen la misma dirección.
Ahora, esto ocurre si los vectores son proporcionales: 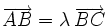
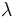 , se obtiene lo que buscamos.
, se obtiene lo que buscamos.Comprueba que los puntos A(2,-1), B(6,1) y C(8,2) están alineados.
Solución:
Para que están alineados los vectores 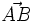 y
y 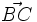 deben ser paralelos, es decir, sus coordenadas deben ser proporcionales:
deben ser paralelos, es decir, sus coordenadas deben ser proporcionales:
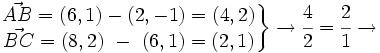 Están alineados.
Están alineados.
Ejercicio resuelto
Averigua el valor de "m" para que P(1,4), Q(5,-2) y R(6,m) estén alineados.
Para que se cumpla lo que piden 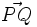 y
y 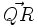 deben ser paralelos, es decir, sus coordenadas deben ser proporcionales.
deben ser paralelos, es decir, sus coordenadas deben ser proporcionales.
- Producto de un escalar por un vector
- Propiedades
- Vectores colineales
- Condición para que tres puntos estén alineados
Ejercicios propuestos
|
Ejercicios propuestos: Puntos y vectores en el plano |
Punto medio de un segmento
Punto medio de un segmento Las coordenadas del punto medio,
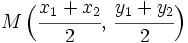 Demostración: Sea
Obtención de la fórmula del punto medio de un segmento AB. Ejemplos Este vídeo explica como se calcula las coordenadas del punto medio de un segmento y lo ilustra con los siguientes ejemplos: 1) Halla el punto medio del segmento de extremos (-17,3) y (5,-29). En este video aprendemos a determinar los puntos que dividen un segmento dado en tres partes iguales. |
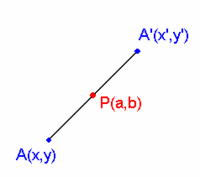
Simétrico de un punto respecto de otro
Para calcular el punto simétrico de un punto respecto de otro, utilizaremos la anterior fórmula del punto medio, tomando como datos los puntos A y M y como incógnita el punto B. Luego despejaremos de las ecuaciones resultantes las coordenadas del punto B.
También podemos hacer uso de la siguiente fórmula:
Ejercicios resueltos
1. Halla el simétrico, A', del punto A(7,4) respecto de P(3,-11).
2. Dados los puntos M(7,4) y N(-2,1), halla un punto P en el segmento MN tal que la distancia de M a P sea la mitad de la distancia de P a N.
Soluciones:
1. A'(-1,-26)
2. P(4,3)Ejercicios propuestos
|
Ejercicios propuestos: Puntos y vectores el plano |
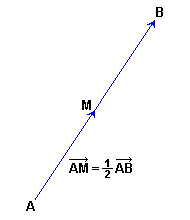
Traslaciones y homotecias
Siendo 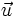 un vector libre, llamamos traslación de vector
un vector libre, llamamos traslación de vector 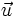 a la transformación que a cada punto A del plano le asocia el punto A' tal que las que las coordenadas del vector fijo
a la transformación que a cada punto A del plano le asocia el punto A' tal que las que las coordenadas del vector fijo 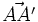 coinciden con las de
coinciden con las de 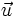 . Del punto A' se dice "trasladado" de A según la traslación de vector
. Del punto A' se dice "trasladado" de A según la traslación de vector 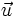 .
Obvio: si u = (u1,u2) y A = (a1,a2), es A' = (a_1+u_1,u_2+u_2).
.
Obvio: si u = (u1,u2) y A = (a1,a2), es A' = (a_1+u_1,u_2+u_2).
Siendo 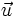 un vector libre, llamamos traslación de vector
un vector libre, llamamos traslación de vector 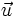 a la transformación que a cada punto A del plano le asocia el punto A' tal que las coordenadas del vector fijo
a la transformación que a cada punto A del plano le asocia el punto A' tal que las coordenadas del vector fijo 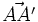 coinciden con las de
coinciden con las de 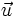 . Del punto A' se dice "trasladado" de A según la traslación de vector
. Del punto A' se dice "trasladado" de A según la traslación de vector 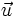 .
Obvio: si
.
Obvio: si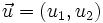 y A = (a1,a2), es A' = (a1 + u1,u2 + u2).
y A = (a1,a2), es A' = (a1 + u1,u2 + u2).
Pueden jugar a darte 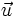 y A y pedirte A', o darte
y A y pedirte A', o darte 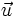 y A' y pedirte A, o darte A y A' y pedirte
y A' y pedirte A, o darte A y A' y pedirte 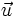 .
.
- Suma de vectores: método del paralelogramo.
- Coordenadas del vector suma.
- Propiedades de la suma de vectores.
- Suma de vectores como composición de traslaciones.
- Llamamos homotecia de centro en el punto "P" y razón "k" a la transformación que a cada punto A del plano le asocia el punto A' tal que el vector fijo
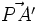 es el producto del número real "k" por el vector fijo
es el producto del número real "k" por el vector fijo 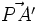 .
.
El punto A' se dice homotético del punto A. Los puntos P, A y A' están alineados.
- La homotecia se dice directa si k>0, y se dice inversa si k<0.
Operaciones con vectores
En éste video jugamos con vectores colineales.
En este video jugamos con la suma de vectores y con el producto escalar de vectores.
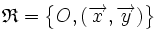

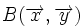
 del plano tiene asociado un vector fijo
del plano tiene asociado un vector fijo 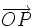
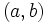 respecto de la base
respecto de la base 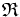
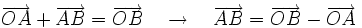
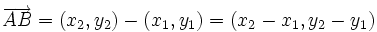
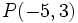 y
y 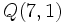 , halla las coordenadas de
, halla las coordenadas de 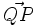 .
.
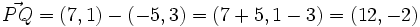
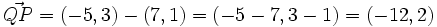
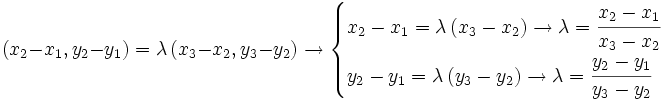
 , de un segmento de extremos
, de un segmento de extremos 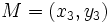 el punto medio del segmento
el punto medio del segmento 
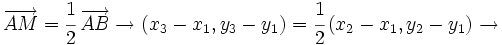
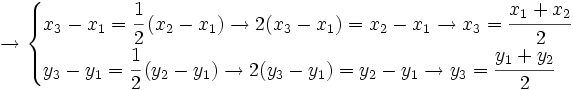
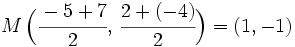
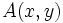 respecto del punto
respecto del punto 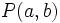 es:
es:
 .
.