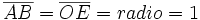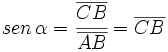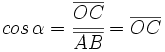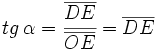Plantilla:Circunferencia goniométrica

De Wikipedia

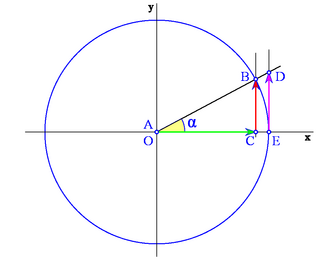
Llamaremos circunferencia goniométrica a la circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con centro en el origen de coordenadas, O.

La circunferencia goniométrica (7´01")     Sinopsis:

Definición y propiedades de la circunferencia goniométrica o circunferencia trigonométrica.

Sobre la circunferencia goniométrica situaremos nuestro ángulo orientado, \alpha \;. Este genera un triángulo rectángulo ABC, tal y como se muestra en la Fig. 2. En él, el vértice A coincide con el origen O, el cateto contiguo al ángulo \alpha \; se situa en el eje X positivo y la hipotenusa coincide con el radio.

Teniendo en cuenta que \overline{AB} = \overline{OE}= radio = 1, las razones trigonométricas del águlo \alpha \; se expresan de la siguiente manera:

  • sen \, \alpha = \cfrac{\overline{CB}}{\overline{AB}}=\overline{CB}
  • cos \, \alpha = \cfrac{\overline{OC}}{\overline{AB}}=\overline{OC}
  • tg \, \alpha = \cfrac{\overline{DE}}{\overline{OE}}=\overline{DE}

Fig. 2: Circunferencia goniométrica: De color rojo, el seno; de color verde, el coseno; de color rosa, la tangente
Aumentar
Fig. 2: Circunferencia goniométrica: De color rojo, el seno; de color verde, el coseno; de color rosa, la tangente

El círculo goniométrico (9´14)     Sinopsis:

Empleando un circulo de radio unidad pueden "visualizarse" las razones trigonométricas de un ángulo orientado.

video
Determinación del ángulo conocida una de sus razones
Tutorial (7´38)     Sinopsis:

Determinación del ángulo conocida una de sus razones empleando el circulo goniométrico.

Ejercicio 1 (5´48")     Sinopsis:

Ejercicio: Conocida una razón trigonométrica, dibujar el ángulo.

Ejercicio 2 (2´46")     Sinopsis:

Ejercicio: Conocida una razón trigonométrica, dibujar el ángulo.

Ejercicio 3 (3´52")     Sinopsis:

Ejercicio: Conocida una razón trigonométrica, dibujar el ángulo.

Ejercicio 4 (8´19")     Sinopsis:

6 ejercicios: Conocida una razón trigonométrica, dibujar el ángulo.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Circunferencia_goniom%C3%A9trica"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda