Plantilla:Tendencias de una función
De Wikipedia
Decimos que una función 
tiende a un valor 
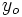cuando la variable independiente tiende a un valor 
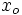, si los valores de la variable 
se acercan a 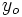cuando la variable 
se acerca a .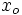
Simbólicamente:
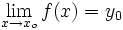
En la anterior expresión la tendencia de la variable independiente puede ser a 
o 
en vez de 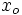. Igualmente, la tendencia de la variable dependiente puede ser a y en vez de a un valor .
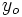Así cuando, por ejemplo, la variable se haga infinitamente grande y los correspondientes valores de la función se acerquen a un valor 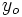, escribiremos:
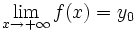
Tendencia de una función Descripción: En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido.
Actividad 1: Tendencias Descripción: Estudia la tendencia del crecimiento de una población de búhos:
En ocasiones nos interesa saber cómo se comporta la función cuando la variable independiente aumenta mucho o disminuye mucho o cuando se acerca a una valor concreto. A los valores a los que se aproxima es lo que llamamos tendencia de la función. Observa la gráfica de la población de búhos (en miles) en un territorio en función del tiempo. Mueve el punto P para ayudarte a contestar las preguntas:
a) ¿Cuál es ese valor? (Nota: En el eje Y, 1 cuadrito = 1 millar de búhos)
Lo mismo ocurre cuando se hace cada vez más negativa la variable independiente, aunque esta tendencia no es el mismo valor.
b) ¿Cuál es ese valor?
Actividad 2: Tendencias Descripción: Estudia la tendencia de la siguiente función:
La tendencia de una función se estudiar también cuando la x se acerca a un número real en vez de a (+/-)infinito. En la escena siguiente recorre la función con el punto P y apunta en tu cuaderno las tendencias de la función.
?
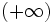b) ¿Y si x se hace muy grande negativamente, es decir, se aproxima a ?
c) ¿A qué valor tiende la función cuando nos aproximamos a 2?
