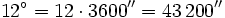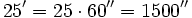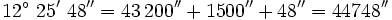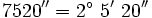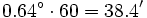Sistema sexagesimal de medida (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
El sistema sexagesimal es un sistema de numeración posicional que emplea como base aritmética el número 60. El número 60 tiene la ventaja de tener muchos divisores como :(1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60), con lo que se facilita el cálculo con fracciones. Nótese que 60 es el número más pequeño que es divisible por 1, 2, 3, 4, 5 y 6.
Tuvo su origen en la antigua Mesopotamia, en la civilización sumeria. También fue empleado por los árabes durante el califato omeya. El sistema sexagesimal se usa para medir tiempos y ángulos principalmente. Su uso se vincula a la vieja astronomía y a la trigonometría.
Medida de ángulos en el sistema sexagesimal
- En el sistema sexagesimal un ángulo completo se divide en 360 partes iguales denominadas grados sexagesimales (se representa 360º).
- Así, un ángulo llano, tendrá la mitad, 180º y uno recto, la cuarta parte, 90º.
Instrumentos de medida de ángulos
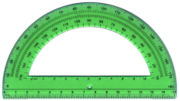
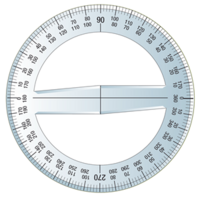
Para medir ángulos sobre un plano utilizamos el transportador. Puede venir en dos presentaciones básicas:
Procedimiento
Actividad en la que podrás ver una representación del círculo goniométrico en el que podras visualizar distintos ángulos cuyas medidas vienen dadas en el sistema sexagesimal. También podrás hacer uso de un transportador de ángulos virtual para empezar a familiarizarte con su manejo. Para trabajos de campo, existen otros instrumentos de medida más precisos, como el teodolito, el goniómetro o el sextante. |
Grados, minutos y segundos sexagesimales
El sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es su sistema de numeración en base 60.
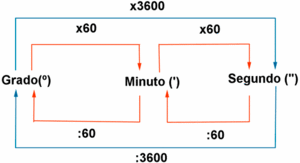
En el sistema sexagesimal un grado se divide en 60 partes iguales denominadas minutos (1º=60'), y cada minuto, en 60 partes iguales denominadas segundos (1'=60")
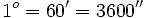
Actividad en la que podrás hacer uso de un transportador de ángulos virtual para aprender a medir ángulos. Además verás cómo los minutos y segundos sexagesimales permiten una mayor precisión en la medida de ángulos.
Forma compleja e incompleja de la medida de un ángulo
La medida de los ángulos se puede expresar:
- En forma compleja: utilizando más de una unidad (grados, minutos y segundos), p.e. 25º 32' 17.
- En forma incompleja o simple: utilizando una sola unidad, p.e. 5,12º.
Procedimiento
|
Ejemplos: Paso de forma compleja a incompleja y viceversa
- Pasa 12º 25' 48" a segundos.
- Pasa 7520" a grados, minutos y segundos.
- Pasa 7.64º a grados, minutos y segundos.
1) Solución:
Sumando todos los segundos:
2) Solución:
Pasamos los segundos a minutos dividiendo por 60:
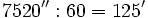 y
y 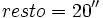
Pasamos los minutos a grados dividiendo por 60:
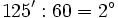 y
y 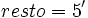
Por tanto:
3) Solución:
Le restamos la parte entera (7º) y pasamos la parte decimal a minutos:
Le restamos la parte entera (38') y pasamos la parte decimal a segundos:
Por tanto:
Videotutorial que explica el paso de medidas incomplejas a complejas de ángulos en el sistema sexagesimal.
Videotutorial que explica el paso de medidas complejas a incomplejas de ángulos en el sistema sexagesimal.
|
Actividad: Ángulos a) Expresa 30.6º en forma compleja. b) Expresa 10º 20' 30" en segundos. b) Expresa 10º 20' en grados. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) 30.6º to degrees b) 10º 20' 30" to arc seconds c) 10º 20' to degrees
|