Plantilla:Espacio muestral
De Wikipedia
← Revisión anterior | Revisión siguiente →
Llamaremos espacio muestral al conjunto formado por todos los resultados o casos de un experimento aleatorio. Lo denotamos con la letra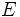 
, o bien, 
.
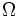Ejemplos: Espacio muestral
a) ¿Cuáles son los casos y el espacio muestral asociado al experimento de "lanzar una moneda"?
b) ¿Cuál es el espacio muestral asociado al experimento de "lanzar dos dados y anotar la suma de los puntos"?
Solución a):
Los casos del experimento aleatorio "lanzar una moneda" son "salir cara" (C) y "salir cruz" (X).
Por tanto, el espacio muestral es
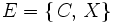
Solución b):
El espacio muestral asociado al experimento de "lanzar dos dados y anotar la suma de los puntos" es:
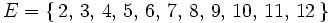
Técnicas de recuento Descripción: Actividades en las que podrás aprender técnicas de recuento para determinar el espacio muestral de un experimento aleatorio.
 Ejercicios: Espacio muestral Describe el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios: a) Lanzar tres monedas. b) Lanzar tres dados y anotar la suma de los puntos obtenidos. c) Extracción de dos bolas de una urna que contiene cuatro bolas blancas y tres negras. d) El tiempo, con relación a la lluvia, que hará durante tres días consecutivos. Ayúdate de la siguiente escena con la que podrás construir el diagrama de árbol correspondiente: Constructor de diagramas de árbol Descripción: Escena que te permite construir diagramas de árbol. Solución: Solución: a) Llamando C a obtener cara y X a la obtención de cruz, obtenemos el siguiente espacio muestral: E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)} b) E={3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18} c) Llamando B a sacar bola blanca y N a sacar bola negra, tenemos: E={BB,BN,NN} d) Si llamamos L al día lluvioso y N al día sin lluvia, para tres días consecutivos se obtiene el siguiente espacio muestral: E={(LLL),(LLN),(LNL),(NLL),(LNN),(NLN),(NNL),(NNN)} |
