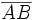Elementos geométricos básicos (1º ESO)

De Wikipedia

Revisión de fecha 11:01 22 mar 2020; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Introducción
2 El plano
3 Puntos y rectas
4 Segmentos y semirrectas
5 Propiedades de las rectas
6 Posiciones relativas de dos rectas

[editar]

Introducción

Para empezar Descripción:

El billar es un juego en el que intervienen muchos de los elementos de la geometría plana (puntos, rectas, ángulos, simetrías ...)

Elementos geométricos básicos (2'54") Sinopsis:

Plano, puntos, segmentos, semirrectas y rectas.

[editar]

El plano

Desde los inicios de la historia, el ser humano ha intentado representar su entorno visual dibujando los objetos y figuras que lo rodean.

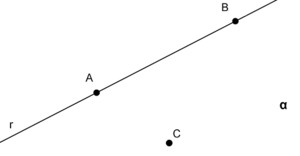
Para ello ha necesitado disponer de alguna superficie sobre la que trazar puntos, líneas, círculos u otras figuras. Desde los petroglifos esculpidos en piedra a las pinturas renacentistas o a los modernos planos utilizados en la arquitectura o la ingeniería, disponemos de innumerables ejemplos de representaciones elaboradas sobre superficies más o menos planas.

El plano es por lo tanto un objeto que cobra importancia para la geometría, ya que nos permite representar figuras sobre él.

Un plano es un objeto ideal que solo posee dos dimensiones, no posee volumen. Se nombran mediante letras griegas: α (alfa), β (beta)...

Representación gráfica informal de un plano.

[editar]

Puntos y rectas

Dentro del plano distinguimos dos elementos fundamentales, tal y como Euclides, considerado como el primer gran matemático de la historia, los definió: el punto y la recta.

Punto: es una figura geométrica sin dimensión. No tiene longitud, ni anchura, ni volumen.
- Sirve para indicar una posición.
- Se nombran con letras mayúsculas: A, B, C,....

Recta: es una figura geométrica unidimensional. Tiene longitud, pero no anchura, ni volumen.
- Contiene un número infinito de puntos que se extienden en una línea siguiendo una misma dirección.
- Se designan mediante dos de sus puntos o mediante una letra minúscula: r, s, t, ...

Junto con el plano, el punto y la recta son considerados "conceptos primarios", es decir, que sólo es posible describirlos en relación con otros elementos similares o parecidos.

Puntos y rectas Descripción:

Actividad de introducción a una herramienta de dibujo que podrás usar a lo largo del tema. Prueba a dibujar puntos y rectas con ella.

Representación gráfica de puntos y recta en el plano.

[editar]

Segmentos y semirrectas

Tomemos dos puntos distintos sobre el plano y unámoslos mediante una línea. Existen desde luego muchas maneras de hacerlo, pero hay una de ellas que es la más corta entre todas las posibles. A esta línea más corta que une dos puntos la llamamos segmento.

Segmento: es la porción de recta comprendida entre dos puntos.
- Si designamos los dos puntos con las letras A y B, designaremos AB al segmento que los une y $\overline{AB}$ a su longitud.
- Los puntos A y B se denominan los extremos del segmento.
Semirrecta: es cada una de las dos partes en que queda dividida una recta al ser cortada en cualquiera de sus puntos.
- Se designan con letras minúsculas.
- Al punto por el que dividimos la recta lo llamaremos origen de las semirrectas.

Representación gráfica de un segmento AB y de una semirrecta, s.

Segmentos y semirrectas Descripción:

Actividad en la que podrás ver y dibujar puntos, segmentos, semirrectas y rectas, utilizando la herramienta de dibujo que antes te presentamos.

Rectas, semirrectas y segmentos

Tutorial (5'38") Sinopsis:

En este video vamos a ver lo que son las rectas, las semirrectas y los segmentos.

Ejercicios (9'46") Sinopsis:

5 ejercicios con rectas, semirrectas y segmentos.

[editar]

Propiedades de las rectas

Existen algunas propiedades de la recta que, a pesar de lo sencillas que resultan absolutamente esenciales para la geometría. Estas son algunas de ellas:

Propiedades

Dados dos puntos distintos en un plano, existe una única recta que los une.
Toda recta divide al plano en dos regiones, llamadas semiplanos.

Propiedades de la recta Descripción:

Actividad en la que podrás visualizar las dos propiedades de la recta que acabamos de ver.

La recta r divide al plano en dos semiplanos.

[editar]

Posiciones relativas de dos rectas

Si trazamos dos rectas sobre el plano, pueden ocurrir varios casos distintos: que coincidan, que se corten en un punto o que no se corten. Así tenemos:

Rectas coincidentes: Son dos rectas que se superponen. Tienen infinitos puntos en común. ( $r = s$ )
Rectas secantes: Son dos rectas que se cortan. Tienen un solo punto en común.
Rectas paralelas: Son dos rectas que no se cortan. No tienen ningún punto en común. ( $r | | s$ )

Posiciones relativas de dos rectas Descripción:

Actividad en la que podrás visualizar las distintas posiciones relativas de dos rectas en el plano.

Propiedad

Por cualquier punto exterior a una recta se puede trazar una única recta paralela a ella.

Recta paralela a otra pasando por un punto (4'39") Sinopsis:

En este vídeo trazamos la paralela a una recta por un punto exterior utilizando regla y compás (2 métodos).

Recta paralela a otra pasando por un punto Descripción:

Actividad en la que podrás ver un video de cómo se traza una paralela a una recta pasando por un punto exterior, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan.

Recta paralela a otra pasando por un punto Descripción:

En esta escena podrás ver cómo se traza una paralela a una recta pasando por un punto exterior, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan.

[editar]

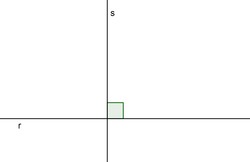
Rectas perpendiculares

Dos rectas son perpendiculares si dividen al plano en cuatro regiones de igual amplitud.

Para indicar que dos rectas son perpendiculares lo representaremos con un cuadradito, tal y como se puede ver en la figura adjunta.

Dada una recta y un punto sobre ella, existe una única recta que contiene a este punto y es perpendicular a la recta, como podrás ver en la siguiente actividad.

Recta perpendicular a otra (8'41") Sinopsis:

En este vídeo trazamos la perpendicular a una recta con regla y compás en distintos casos.

Recta perpendicular a otra pasando por un punto Descripción:

Actividad en la que podrás ver un video de cómo se traza una perpendicular a una recta pasando por un punto, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan.
Ejercicios resueltos sobre los elementos geométricos básicos vistos en este tema.

Recta perpendicular a otra pasando por un punto Descripción:

En esta escena podrás ver cómo se traza una perpendicular a una recta pasando por un punto, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan.

Rectas perpendiculares.

[editar]

Distancia entre dos rectas paralelas

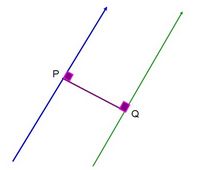
La distancia de un punto a una recta es la longitud del segmento perpendicular del punto a la recta.
La distancia ente dos rectas paralelas es la distancia de cualquier punto de una a la otra.