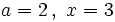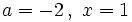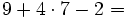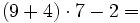Biblioteca de plantillas
De Wikipedia
Tabla de contenidos |
Menús
Menú Desplegable
| Ir a | Para repasar | Para ampliar | Herramientas |
| Indice | Tablas multiplicar | Números naturales | WIRIS |
Menú Derecha
| NUMEROS NATURALES |
| Ir a |
| Para ampliar |
| Para repasar |
| Herramientas |
Menú Asignatura
| Enlaces |
| Descartes WIRIS Geometría (E.S.O.) |
| Ejercicios |
| E.S.O. Bachillerato |
| Multimedia |
| {{{multimedia}}} |
| Documentos |
| Exámenes Programaciones |
Tablas
Tablabonita
| Peso (kg) | Precio (€) |
|---|---|
| 1 | 1,5 |
| 2 | 3 |
| 3 | 4,5 |
Tablabonitablanca
| Peso (kg) | Precio (€) |
|---|---|
| 1 | 1,5 |
| 2 | 3 |
| 3 | 4,5 |
Tabla75
| 1 | 2 |
Tabla50
| 1 | 2 |
Tabla3
| 1 | 2 | 3 |
Tabla4
| 1 | 2 | 3 | 4 |
Wiris
Video
Video enlace
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.
Video enlace 2
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.
Video1
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Video2
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Video2b
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Web
{{{descripcion}}}
Web: Phi el número de oro
Web de Luis Nicolás Ortiz.
MP3
Calculadora
|
Calculadora: Notación científica |
Teoremas
Teorema
Teorema sin demo
Ejemplos
Ejemplo_simple (sin caja)
Ejemplo (con solución)
Ejemplo2 (sin solución)
Ejemplos múltiples
Ejemplos: Ecuaciones trigonométricas
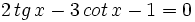
Transformamos la ecuación de partida:
Hacemos un cambio de variable: 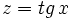
Soluciones:
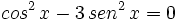
Usando la identidad fundamental:
Sustituimos en nuestra ecuación de partida:
Soluciones:
Compositores
Ejercicios
Actividad (sin solución)
|
Actividad 1
|
Wolfram
|
Actividad: Valor numérico de una expresión algebraica |
Wolfram
|
Actividad: Valor numérico de una expresión algebraica 1. Calcula:
Solución: |
Ejercicios (con solución)
|
Ejercicios 1. Calcula:
Solución: a) 35 b) 89 c) 29 d) 65
2. En una división, el dividendo es 969, el cociente 74, y el resto 7. ¿Cúal es el divisor?
Solución: El divisor es 13 |
Ecuación (con número de referencia)
| Aquí vendría la fórmula | (Num. Ref.) |
Cajas
Caja Amarilla
Este es el contenido
Caja
|
Aquí vendría la fórmula |
Actividad interactiva
AI enlace
Un poco de historia sobre el papiro de Rhind. Las fracciones unitarias.
AI
AI2
|
Actividades Interactivas: Formas de expresar una función
1. Variable discreta.
Actividad:
2. Variable continua.
Actividad: El siguiente ejemplo es muy similar al anterior. Queremos comprar patatas a 0,30 € el kilo. Podemos construir una tabla y una gráfica idénticas a las anteriores salvo que en el eje horizontal representamos los kilos de patatas. |
AI3
Desplegables
Desplegable
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Desplegable2
Sea AB un diámetro de la circunferencia: 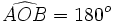 . Por el apartado a), el ángulo inscrito
. Por el apartado a), el ángulo inscrito 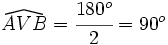 .
.
Tarea
Eventos calendario
Sintaxis:
{{Evento
|tipo=Puede ser uno de los 4 siguientes: Tarea, Examen, Act.Extraescolar, Otros
|asignatura=Asignatura
|contenido=Explicación del evento
}}
Ejemplos

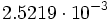

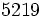

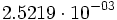
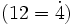 porque
porque 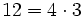 . Por tanto, 4 es divisor de 12
. Por tanto, 4 es divisor de 12 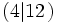 .
.
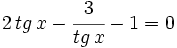
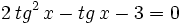
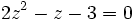
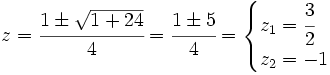
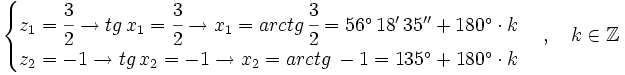
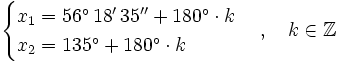
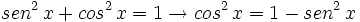
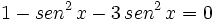
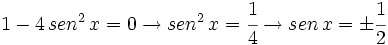
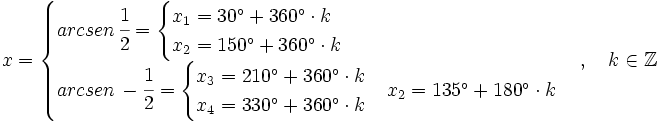
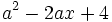 en los casos:
en los casos: