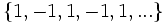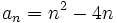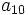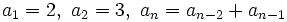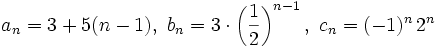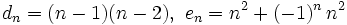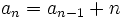Concepto de sucesión (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sucesión de números reales
(pág. 52)
Una sucesión de números reales es una función  , que a cada número natural
, que a cada número natural  le asocia un número real
le asocia un número real 
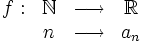
Esto genera el conjunto ordenado
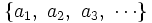
que se llaman los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos 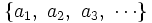 en lugar de la sucesión
en lugar de la sucesión  .
.
Ejercicios resueltos: Concepto de sucesión
- Descubre el criterio por el que se forman las sucesiones siguientes y añade dos términos más a cada una:
- a)
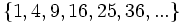
- b)
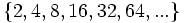
- c)
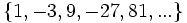
- d)
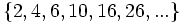
- e)
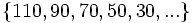
- f)
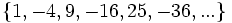
- a)
- a) Cada término es el cuadrado del lugar que ocupa.
- b) Cada término, a partir del segundo, se obtiene multiplicando por 2 el anterior.
- c) Cada término, a partir del segundo, se obtiene multiplicando por -3 el anterior.
- d) Cada término, a partir del tercero, se obtiene sumando los dos anteriores.
- e) Cada término, a partir del segundo, se obtiene restándo 20 al anterior.
- f) Los términos pares, a partir del segundo, se obtienen sumando 2 al anterior.
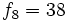
- y los términos impares, a partir del tercero, se obtienen multiplicando por 2 el anterior.
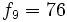
Ejercicios
(pág. 52)
|
Ejercicios propuestos: Concepto de sucesión |
La sucesión de Fibonacci y el número áureo
Ejemplo: La sucesión de Fibonacci y el número áureo
El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo (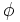 ):
):
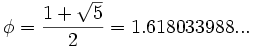
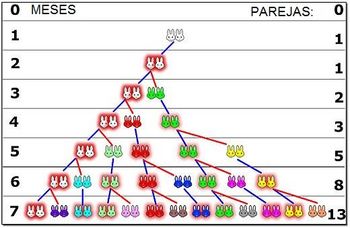
a) Sucesión de Fibonacci:
- Mes 1: 1 pareja (la pareja nace al comenzar el primer mes)
- Mes 2: 1 pareja (la pareja no es fértil hasta que termine el 2º mes)
- Mes 3: 2 parejas (al comenzar el tercer mes se reproduce por primera vez)
- Mes 4: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el comienzo del próximo mes)
- Mes 5: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 6: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 7: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene la sucesión de Fibonacci, en la que cada término se obtiene a partir de la suma de los dos anteriores:
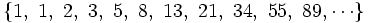
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos la sucesión:
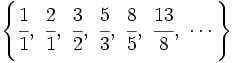
que expresada con decimales vemos que se aproxima al número áureo:
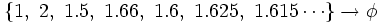
Nota: Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la parición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteamiento recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático.
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
Grandes temas de la matemática - Capítulo 4: Fibonacci. (con Adrian Paenza)
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
Grandes temas de la matemática - Capítulo 4: Fibonacci. (con Adrian Paenza)
Término general de una sucesión
(pág. 53)
Se llama término general de una sucesión, y se simboliza por  , al término que representa a uno cualquiera de ella. La sucesión correspondiente se representa de forma abreviada por
, al término que representa a uno cualquiera de ella. La sucesión correspondiente se representa de forma abreviada por 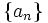
- Hay veces que el término general se puede expresar mediante una fórmula:
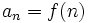 . Dándole a n un valor, se obtiene el término correspondiente.
. Dándole a n un valor, se obtiene el término correspondiente.
- Otras veces, cada término de la sucesión se obtiene a partir de operaciones con otros términos anteriores. A estas sucesiones se les llama recurrentes. En ellas, para hallar un término, tenemos que hallar todos los anteriores. En estos casos se suele dar una ley de recurrencia, una regla que relaciona cada término con sus anteriores.
Ejercicios resueltos: Término general de una sucesión
- Halla el término general (si se puede) o la ley de recurrencia de las siguientes sucesiones:
- a)
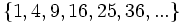
- b)
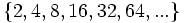
- c)
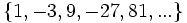
- d)
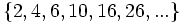
- e)
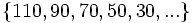
- f)
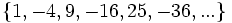
- a)
- a)
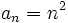
- b)
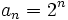
- c)
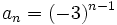
- d) Es recurrente. La ley de recurrencia es
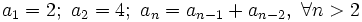
- e)
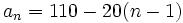
- f)
|
Actividad: Termino general de una sucesión
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
(pág. 53)
Videotutoriales sobre sucesiones
El concepto de función o aplicación ente dos conjuntos es necesario para la definición de sucesión.
- Definición de sucesión de números reales como aplicación entre el conjunto de los números naturales y el de los números reales.
- Término general de una sucesión.
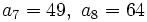
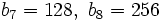
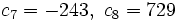
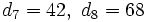
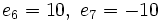
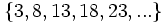
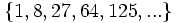
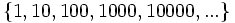
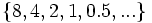
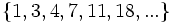
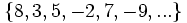
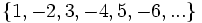
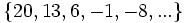

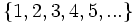 b)
b) 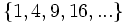 c)
c) 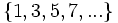
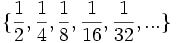 e)
e) 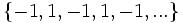 f)
f)