Plantilla:Cota error
De Wikipedia
Para que la cantidad aproximada que utilizamos sea fiable, el error cometido debe estar controlado o acotado. Las cotas de error nos darán el máximo error que cometeremos al dar una aproximación de un número.
- Llamaremos cota del error absoluto a un número k que cumpla que E.A. < k.
- Llamaremos cota del error relativo a un número k´ que cumpla que E.R. < k´.
Cotas del error absoluto y relativo
Cuando redondeamos un valor, podemos dar cotas de los errores de la siguiente manera:
- Cota de error absoluto: k = 5 unidades del orden de la primera cifra no utilizada en el redondeo.
- Cota del error relativo: k´ =
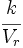
- Cota de error absoluto: k = 5 unidades del orden de la primera cifra no significativa.
- Cota del error relativo: k´ =
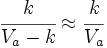
Ejemplo: Cota del error
a) Una montaña mide 2475 m. Halla la cota de los errores absoluto y relativo cometidos en el redondeo a las centenas.
b) Una montaña (que no se sabe lo que mide ralmente) mide, aproximadamente, 2500 m (esta sería la cantidad redondeada). Halla la cota de los errores absoluto y relativo.
Redondeando a las centenas, la montaña mide 2500 m. a) Al redondear la primera cifra no utilizada es la de las decenas. De esta forma, la cotas de error son:
- Cota de error absoluto: k = 50
- Cota del error relativo: k´ =
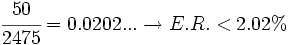
b) Como la cantidad redondeada es 2500 m, la primera cifra no significativa es la de las decenas. De esta forma, la cotas de error son:
- Cota de error absoluto: k = 50
- Cota del error relativo: k´ =
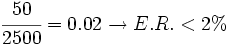
Corolario
Cuantas más cifras significativas se utilicen para dar una medida aproximada, menor es el error relativo cometido.
Ejercicios resueltos:
1. La altura de un edificio es de 92 m; la de un avión, 9.2 km, y la de un satélite artificial, 920 km. ¿Qué podemos decir del error absoluto y del error relativo de estas mediciones?
2. Comparar el error relativo cometido en estas mediciones:
- a) 87 m b) 5 km c) 453 km d) 4.53·1011 km
Solución 1. El mayor error relativo se da en el apartado b), ya que sólo tiene una cifra significativa.
El menor error relativo se da en el apartado c) y d) (ambos con igual error relativo), por tener tres cifras significativas.
Solución 2. La cota del error absoluto es 5 unidades de la primera cifra no significativa:
- Altura edificio: V.Aprox. = 92 m; E.A. < 0.5 m
- Altura avión: V.Aprox. = 9.2 km; E.A. < 0.05 km = 50 m
- Altura satélite: V.Aprox. = 920 km; E.A. < 5 km = 5000 m
El menor error absoluto se da en la medición de la altura del edificio y el mayor, en la del satélite.
El error relativo es el mismo en los tres casos, ya que todas las mediciones usan 2 cifras significativas. Vamos a comprobarlo de todas formas:
- Altura edificio: V.Aprox. = 92 m; E.A. < 0.5; E.R. < 0.5/92
- Altura avión: V.Aprox. = 9.2 km; E.A. < 0.05 km = 50 m; E.R. < 0.05/9.2 = 0.5/92
- Altura satélite: V.Aprox. = 920 km; E.A. < 5 km = 5000 m; E.R. < 5/920 = 0.5/92
Videotutorial sobre las cotas de error absoluto y relativo.

