Funciones: Introducción (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Introducción
- El análisis matemático es una rama de las matemáticas que estudia los números reales, los complejos y las funciones entre esos conjuntos. Se empieza a desarrollar a partir de de la formulación rigurosa de límite y estudia conceptos como la continuidad, la integración y la derivación.
- El cálculo infinitesimal o simplemete Cálculo es una rama del análisis matemático que se divide en dos áreas: cálculo diferencial y cálculo integral.
- El cálculo diferencial es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada.
- El cálculo diferencial es una parte del análisis matemático que consiste en el estudio de las integrales. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños.
Una de las diferencias entre el álgebra y el análisis es que en este segundo recurre a construcciones que involucran sucesiones de un número infinito de elementos, mientras que álgebra usualmente es finitista.
- Introducción al cálculo diferencial.
Sin duda Newton es el autor del primer paso de la carrera espacial. Las Leyes descubiertas por él son las que han permitido al hombre poner un pie en la Luna o enviar naves a Marte y Venus, explorar los planetas exteriores: Júpiter, Saturno, Neptuno y Urano. Su modelo de telescopio ha permitido ver más lejos en cielo. Sin duda los astrónomos le deben mucho a Newton. Pero los matemáticos, y de paso el resto de los científicos, le deben tanto o más. Él junto a Leibniz, aunque sería mejor decir al mismo tiempo que Leibniz, son los descubridores de la más potente y maravillosa herramienta matemática: el Cálculo. Newton tuvo en vida un prestigio y un reconocimiento social aún mayor que el que pudo tener Einstein en nuestro siglo. Como los reyes y muy pocos nobles fue enterrado en la abadía de Westminster. Leibniz murió sólo y abandonado por todos. A su entierro en Hannover sólo asistió su criado. Hoy los dos comparten por igual la gloria de ser los padres de las dos herramientas más potentes del universo matemático: el cálculo diferencial y el cálculo integral. El instrumento ideal para entender y explicar el funcionamiento del mundo real, desde las cosas más próximas hasta el rincón más alejado del universo.
Una breve historia de las funciones
En las matemáticas actuales el concepto de función se define del modo siguiente:
Sean A y B conjuntos. Se llama función entre A y B a cualquier relación establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B.
Para representar las funciones se suele utilizar la notación 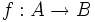 para los conjuntos,
para los conjuntos,  para los elementos. A se llama conjunto inicial y B es el conjunto final.
para los elementos. A se llama conjunto inicial y B es el conjunto final.
Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En los próximos temas vamos a estudiar funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final)
de variable real (conjunto inicial), 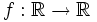 .
.
El concepto de función se desarrolló con el paso del tiempo; su significado fue cambiando y también la forma en que se definía, ganando precisión a través de los años.
Comenzaremos en Mesopotamia. En las matemáticas babilónicas encontramos tablas con los cuadrados, los cubos y los inversos de los
números naturales. Estas tablas sin duda definen funciones de 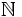 en
en 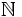 o de
o de 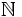 en
en  , lo que no implica que los babilonios conocieran el concepto de función. Conocían y
manejaban funciones específicas, pero no el concepto abstracto y moderno de función.
, lo que no implica que los babilonios conocieran el concepto de función. Conocían y
manejaban funciones específicas, pero no el concepto abstracto y moderno de función.
En la Grecia clásica también manejaron funciones particulares —incluso en un sentido moderno de relación entre los elementos de dos conjuntos y no sólo de fórmula— pero es poco probable que comprendieran el concepto abstracto moderno de función.
La mayor parte de los historiadores de las matemáticas parecen estar de acuerdo en atribuir a Nicole Oresme (1323-1382) la primera aproximación al concepto de función, cuando describió las leyes de la naturaleza como relaciones de dependencia entre dos magnitudes. Fue el primero en hacer uso sistemático de diagramas para representar magnitudes variables en un plano.En la revolución científica iniciada en el siglo XVI los científicos centraron su atención en los fenómenos de la naturaleza, poniendo énfasis en las relaciones entre las variables que determinaban dichos fenómenos y que podían ser expresadas en términos matemáticos. Era necesario comparar las variables, relacionarlas, expresarlas mediante números y representarlas en algún sistema geométrico adecuado.
Galileo Galilei (1564-1642) pareció entender el concepto de función aún con mayor claridad. Sus estudios sobre el movimiento contienen la clara comprensión de una relación entre variables.
Casi al mismo tiempo que Galileo llegaba a estas ideas, Renè Descartes (1596-1650) introducía la geometría analítica. Descartes desarrolló y llevó a sus fundamentales consecuencias las ideas que siglos atrás se habían usado para representar en el plano relaciones entre magnitudes. Ahora cualquier curva del plano podía ser expresada en términos de ecuaciones y cualquier ecuación que relacionara dos variables podía ser representada geométricamente en un plano.
A finales del siglo XVII aparece por primera vez el término función. En palabras de Johan Bernoulli, una función es “una cantidad formada de alguna manera a partir de cantidades indeterminadas y constantes”.
Pero no fue hasta 1748 cuando concepto de función saltó a la fama en matemáticas. Leonhard Euler, uno de los grandes genios de las matemáticas de todos los tiempos, publicó un libro, Introducción al análisis infinito, en el definió función como:
Una función de una cantidad variable es una expresión analítica compuesta de cualquier manera a partir de la cantidad variable y de números o cantidades constantes.
Pero Euler no define expresión analítica. Así que poco después, en 1755, tuvo que precisar su definición:
Si algunas cantidades dependen de otras de tal modo que si estas últimas cambian también lo hacen las primeras, entonces las primeras cantidades se llaman funciones de las segundas.
Pero la cosa seguía sin estar clara del todo: ¿cómo es esa dependencia?, ¿cómo expresarla, calcularla o representarla?, ¿cómo deben cambiar los valores de las variables?, ¿cuántas variables pueden intervenir?. Muchos matemáticos abordaron el problema de dar una definición precisa y adecuada de función. Y así se pasaron casi dos siglos, puliendo poco a poco el concepto, hasta que, ya en el siglo XX, Edouard Goursat dio en 1923 la definición que aparece en la mayoría de los libros de textos hoy en día:
Se dice que y es una función de x si a cada valor de x le corresponde un único valor de y. Esta correspondencia se indica mediante la ecuaci ón y = ƒ(x)
Historia de las funciones (Parte 1)
Historia de las funciones (Parte 2)



