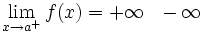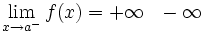Plantilla:Ramas infinitas. Asíntotas (1ºBach)

De Wikipedia

Tabla de contenidos

Ramas infinitas

Decimos que una función f(x)\; presenta una rama infinita si:

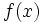  1. f(x)\, tiende a +/- infinito cuando x tiende a un punto.
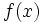  2. f(x)\, tiende a +/- infinito cuando x tiende a (+/-) infinito.
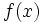  3. f(x)\, tiende a un número real cuando x tiende a (+/-) infinito.

Cuando la rama infinita se aproxima a una recta, recibe el nombre de asíntota.

Ramas infinitas cuando x tiene a un punto: Asíntotas verticales

Una función f(x)\; presenta en x=a\; una asíntota vertical (A.V.) si ocurre alguna de estas dos cosas:

\lim_{x \to a^+} f(x)=+ \infty \ ó \ -\infty
\lim_{x \to a^-} f(x)=+ \infty \ ó \ -\infty

La gráfica de la función se acerca a la recta x=a\; (asíntota vertical), al aproximarse la variable x\; al punto x=a\;.

Ramas infinitas cuando x tiene a infinito

Ejercicios propuestos

ejercicio

Ejercicios propuestos: Ramas infinitas

(Pág. 287)

1

Ramas infinitas de las funciones racionales

Ejercicios propuestos

ejercicio

Ejercicios propuestos: Ramas infinitas de las funciones racionales

(Pág. 289)

1

Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas

Ejercicios propuestos

ejercicio

Ejercicios propuestos: Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas

(Pág. 290)

1

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Ramas_infinitas._As%C3%ADntotas_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda