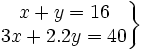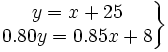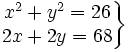Plantilla:Resolución de problemas mediante sistemas
De Wikipedia
Procedimiento
Para resolver un problema mediante sistemas de ecuaciones hay que seguir los siguientes pasos:
- Determinar las incógnitas.
- Traducir el enunciado del problema al lenguaje algebraico mediante ecuaciones en las que intervengan las incógnitas.
- Resolver el sistema, es decir, hallar el valor de las incógnitas.
- Dar la solución del problema a partir de los valores obtenidos de las incógnitas.
Ejercicios resueltos
- Dos estaciones A y B distan 255 km. Un tren sale de A hacia B a una velocidad constante de 60 km/h. Simultáneamente, sale de B hacia A otro tren a 110 km/h. Calcular el tiempo que tardan en cruzarse y la distancia que ha recorrido cada uno hasta ese instante.
- Un bodeguero ha mezclado dos garrafas de vino. La primera, de mejor calidad, a 3 €/l y la segunda, de claidad inferior, a 2.20 €/l. De esta forma ha obtenido 16 l de un vino de calidad intermedia que sale a 2.50 €/l. ¿Qué cantidad de vino había en cada garrafa?
- Mariluz ha comprado un abrigo que estaba rebajado un 15%. Jorge ha comprado otro abrigo 25 € más caro, pero ha conseguido una rebaja del 20%, con lo que sólo ha pagado 8 € más que Mariluz. ¿Cuál era el precio original de cada abrigo?
- La diagonal de un rectángulo mide 26 m, y el perímetro, 68 m. Calcula la medida de sus lados.
Solución 1:
- x = distancia de A al punto de encuentro de los dos trenes.
- 255-x = distancia de B al punto de encuentro de los dos trenes.
- Primer tren:
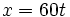
- Segundo tren:
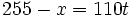
- Sol: x = 90 ; t = 1.5
Los trenes se encuentran 1h 30 min después de salir. El primer tren recorre 90 km y el segundo 165 km.
Solución 2:
- x = litros de vino de mejor calidad
- y = litros de vino de calidad inferior
- Sol: x = 6 ; y = 10
Había 6 l en la primera garrafa y 10 l en la segunda.
Solución 3:
- x = precio del abrigo de Mariluz sin rebajar
- y = precio del abrigo de Jorge sin rebajar
- Sol: x = 240 ; y = 265
El abrigo de Mariluz costaba 240 € y el de Jorge 265 €.
Solución 4:
- x = base del rectángulo
- y = altura del rectángulo
El sistema tiene dos soluciones:
- x = 24 ; y = 10
- x = 10 ; y = 24
Actividad 1a Descripción: Actividades en las que aprenderás y practicarás la resolución de problemas de distintos tipos mediante sistemas de ecuaciones lineales con dos incógnitas.
Actividad 1b Descripción: Problemas resueltos mediante sistemas de ecuaciones lineales con dos incógnitas.
Autoevaluación Descripción: Problemas que se resuelven mediante sistemas de ecuaciones lineales con dos incógnitas.
Problemas resueltos Descripción: Problemas resueltos mediante sistemas de ecuaciones lineales con dos incógnitas.
