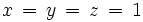Método de Gauss para sistemas lineales (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Método reducción de Gauss
El método de Gauss se debe al matemático alemán Johann Carl Friedrich Gauss. Consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante operaciones elementales por filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.
Ejemplo: Método de reducción de Gauss
- Resuelve el siguiente sistema de ecuaciones por el método de Gauss:
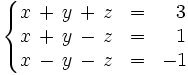
La matriz ampliada del sistema de ecuaciones es:
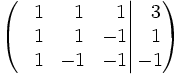
Si a la tercera y segunda fila le restamos la primera, obtenemos:
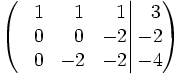
Si ahora intercambiamos la segunda y tercera filas, obtenemos

que es la matriz ampliada del sistema de ecuaciones:
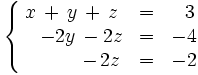
que es equivalente al inicial.
Solucionamos la tercera ocuacion para obtener 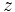 :
:
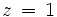
En la primera y segunda ecuación, sustituimos 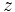 por la solucion de la tercera ecuación (
por la solucion de la tercera ecuación (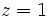 ), para obtener:
), para obtener:
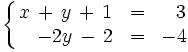
La segunda ecuación es ahora una ecuación con una sola incognita  , que resolvemos para obtener:
, que resolvemos para obtener:
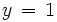
Sustituimos la incógnita  de la primera ecuación, por la solución obtenida en la segunda ecuación (
de la primera ecuación, por la solución obtenida en la segunda ecuación (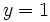 ). Esto nos da una ecuación en
). Esto nos da una ecuación en  :
:
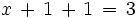
que al resolverla termina de darnos la solución del sistema de ecuaciones inicial: