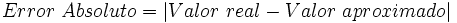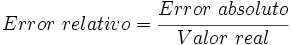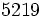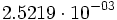Expresión decimal de los números reales. Aproximaciones (1ºBach)

De Wikipedia

Revisión de fecha 22:13 9 ene 2009; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Geogebra Calculadoras

Tabla de contenidos

1 Expresión decimal de los números reales
2 Aproximaciones
- 2.1 Redondeo
- 2.2 Truncamiento
3 Errores
- 3.1 Error absoluto
- 3.2 Error relativo
4 Cota del error
- 4.1 Redondeo y cota del error
5 Notación científica
- 5.1 La notación científica en la calculadora

Expresión decimal de los números reales

Cuando escribimos el número 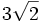$3\sqrt2$ queda reflejado con total precisión de que número estamos hablando. Este número, tan sencillo de expresar con radicales, tiene, sin embargo, una expresión decimal que consta de infinitas cifras (4.2426406871192851464050661726291...). En la práctica, muchas veces es preferida la expresión decimal aproximada, con una cantidad reducida de cifras decimales (4.24), aunque ésta sea imprecisa, porque resulta más fácil captar su valor que expresándolo con radicales.

Aproximaciones

Cuando un número tiene muchas cifras, es difícil recordarlo y operar con él. Por eso lo solemos sustituir por otro más manejable de valor similar, prescindiendo de sus últimas cifras, que sustituimos por ceros. Ese otro número más sencillo decimos que es una aproximación del número de partida.
Cuando aproximamos un número, nos quedamos con sus primeras cifras y completamos con ceros. Esas cifras, con las que nos quedamos, se llaman cifras significativas.
Llamamos orden de la aproximación, a la posición hasta la que nos quedamos con cifras significativas.
Se puede aproximar por defecto si el número utilizado es menor que el de partida, o por exceso si el número utilizado es mayor que el de partida.

Ejemplo: Aproximaciones

Aproxima por defecto y por exceso los siguientes números:

a) 263825 con 2 cifras significativas.

b) 6035192 con 1 cifra significativa.

c) 60,35 con 3 cifras significativas.

Solución:

   Número         Aproximación        Aproximación       Nº cifras          Orden de la
 de partida       por defecto          por exceso      significativas       aproximación
 ------------     ------------      --------------     --------------    -------------------
    263825    --->    260000   --->      270000    --->       2      ---> Decenas de millar
   6035192    --->   6000000   --->     7000000    --->       1      ---> Unidades de millón
        60,35 --->        60,3 --->          60,4  --->       3      ---> Décimas

Redondeo

Para redondear un número a un determinado orden de unidades:

Se sustituyen por ceros todas las cifras a la derecha de dicho orden
Si la primera cifra sustituida es mayor o igual que cinco se suma una unidad a la cifra anterior

Ejemplo: Redondeo

Redondea los siguientes números:

a) 27640,342 a la centena.

b) 3857,567 a la décima.

c) 24572,2578 a la unidad de millar.

Solución:

a) 27600 ; b) 3857,6 ; c) 25000

Truncamiento

Para truncar un número a un determinado orden de unidades se sustituyen por ceros todas las cifras a la derecha de dicho orden.

Ejemplo: Truncamiento

Trunca los siguientes números :

a) 27630,24578 a la milésima.

b) 3851,34 a la unidad.

c) 12345621,2 a la decena de millar.

Solución:

a) 27630,245 ; b) 3851 ; c) 12340000

Errores

Cuando damos una cantidad de forma aproximada, cometemos un error. Distinguiremos los siguientes tipos de errores:

Error absoluto

El error absoluto es la diferencia entre el valor real y el aproximado, en valor absoluto, es decir, siempre con signo positivo.

$Error \ Absoluto= |Valor \ real - Valor \ aproximado|$

Ejemplo: Error absoluto

Una montaña mide 2475 m. Redondea la altura a las centenas y halla el error absoluto cometido:

Solución:

a) Redondeando a las centenas, la montaña mide 2500 m.

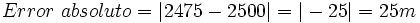
b) $Error \ absoluto = |2475 - 2500| = |-25| = 25 m$

Error relativo

El error relativo es el cociente entre el error absoluto y el valor exacto.

$Error \ relativo= \cfrac {Error \ absoluto}{Valor \ real}$

Ejemplo: Error relativo

Una montaña mide 2475 m. Trunca la altura a las centenas y halla el error relativo cometido:

Solución:

a) Truncando a las centenas, la montaña mide 2400 m.

b) 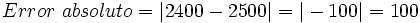$Error \ absoluto = |2400 - 2500| = |-100| = 100$

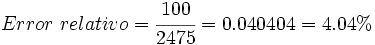
c) $Error \ relativo= \cfrac {100}{2475}=0.040404=4.04%$

Actividades Interactivas: Errores

1. Ejemplos sobre aproximaciones de fracciones y los errores cometidos.

Actividad:

En la siguiente escena se muestran ejemplos de como se redondea ó trunca una fracción a un orden determinado de decimales, así como los errores absoluto y relativo cometidos.

Pulsa "Inicio" para obtener un nuevo ejemplo.

Introduce el orden de la aproximación en la casilla correspondiente y pulsa "Redondeo" o "Truncamiento" para obtener distintos tipos de aproximaciones.

Anota algún ejemplo en tu cuaderno.

Click aquí si no se ve bien la escena

2. Ejercicios sobre aproximaciones de fracciones y los errores cometidos.

Actividad:

Pulsa el botón "Ayuda" y lee atentamente la explicación del ejercicio.

Click aquí si no se ve bien la escena

Cota del error

Para que la cantidad aproximada que utilizamos sea fiable, el error cometido debe estar controlado o acotado de manera que:

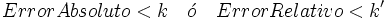
$Error Absoluto<k \quad \acute{o} \quad Error Relativo<k'$

Los números k y k' se llaman cotas del error absoluto o relativo, respectivamente.

Redondeo y cota del error

Al redondear, podemos dar una cota del error absoluto de la siguiente manera:

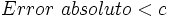
$Error \ absoluto < c$

donde c = 5 unidades del orden de la primera cifra no utilizada en el redondeo.

Y una cota del error relativo:

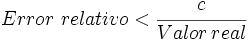
$Error \ relativo < \cfrac{c}{Valor \, real}$

Ejemplo: Cota del error

En el ejemplo anterior de la montaña que mide 2475 m, halla la cota de los errores absoluto y relativo cometidos en el redondeo a las centenas.

Solución:

Redondeando a las centenas, la montaña mide 2500 m. Al redondear la primera cifra no utilizada es la de las decenas. De esta forma, la cota del error cometido es 50.

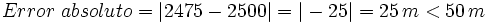
$Error \ absoluto = |2475 - 2500| = |-25| = 25 \, m < 50 \, m$

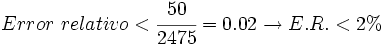
$Error \ relativo < \cfrac{50}{2475}=0.02 \rightarrow E.R.< 2%$

Notación científica

Trabajar con números muy grandes o muy pequeños resulta engorroso. Por eso debemos aprender a escribir estos números de una forma más abreviada y que resulte más cómoda. Para ello nos ayudaremos de lo que hemos visto sobre las potencias de 10.

Esta forma de escribirlos es lo que llamaremos notación científica, cuestión que pasaremos a explicar a continuación.

Un número está en notación científica si aparece expresado de la forma:

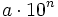
$a \cdot 10^n$

donde $a \;\!$ es un número con 1 cifra entera distinta de cero y un número cualquiera de decimales.

La notación científica en la calculadora

La mayoría de las calculadoras expresan los números en notación científica omitiendo la potencia de 10, mostrando sólo el número que va multiplicando delante del 10 y el exponente.

La siguiente actividad te ayudará a entenderlo:

Actividade Interactiva: Notación científica con calculadora

1. Interpretando la notación científica en la calculadora.

Actividad:

Pulsa "INICIO" y, a continuación, pulsa uno de los tres botones inferiores, pero sólo uno.

Escribe en tu cuaderno las tres formas posibles y comprueba tus soluciones pulsando los otros dos botones inferiores.

Anota los resultados en tu cuaderno.

Click aquí si no se ve bien la escena

Ahora efectúa en tu calculadora científica las siguientes operaciones y expresa el resultado en notación científica en tu cuaderno: