Límite de una función en un punto (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Límite de una función en un punto
El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto.
Aproximación a un punto
- Decimos que
 tiende a
tiende a  por la izquierda (
por la izquierda (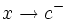 ) cuando a
) cuando a  se le dan valores menores que
se le dan valores menores que  , cada vez más próximos a
, cada vez más próximos a  .
.
- Decimos que
 tiende a
tiende a  por la derecha (
por la derecha (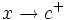 ) cuando a
) cuando a  se le dan valores mayores que
se le dan valores mayores que  , cada vez más próximos a
, cada vez más próximos a  .
.
- Decimos que
 tiende a
tiende a  (
( ) cuando a
) cuando a  se le dan valores cada vez más próximos a
se le dan valores cada vez más próximos a  .
.
- Los puntos en la recta real.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
 y
y  .
.
- Concepto de distancia entre dos puntos.
- Concepto de entorno de un punto.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
 y
y  .
.
Límites laterales y límite de de una función en un punto
Dada una función  , cuando la variable independiente
, cuando la variable independiente  se aproxima a un cierto punto
se aproxima a un cierto punto  , ya sea por la derecha o por la izquierda,
, ya sea por la derecha o por la izquierda,  va tomando valores que pueden aproximarse o no a un cierto punto. Diremos que:
va tomando valores que pueden aproximarse o no a un cierto punto. Diremos que:
- Una función
 tiene límite por la izquierda en un punto
tiene límite por la izquierda en un punto  , si existe un número
, si existe un número  , de manera que cuando
, de manera que cuando 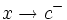 , los correspondientes valores
, los correspondientes valores 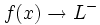 . Lo representaremos:
. Lo representaremos:
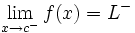
- Una función
 tiene límite por la derecha en un punto
tiene límite por la derecha en un punto  , si existe un número
, si existe un número 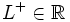 , de manera que cuando
, de manera que cuando 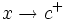 , los correspondientes valores
, los correspondientes valores 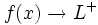 . Lo representaremos:
. Lo representaremos:
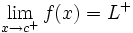
- Una función
 tiene límite en un punto
tiene límite en un punto  , si existe un número
, si existe un número 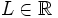 de manera que tanto su límite por la derecha, como su límite por la izquierda, existen y coinciden con
de manera que tanto su límite por la derecha, como su límite por la izquierda, existen y coinciden con 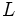 , es decir, cuando
, es decir, cuando 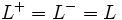 . Simbólicamente:
. Simbólicamente:
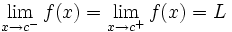
- Recordando el concepto de función.
- Conceptos de límite de una función por la derecha y por la izquierda de un punto.
- Concepto de límite de una función en un punto.
- Se puede calcular el límite en un punto independientemente de que el punto pertenezca o no al dominio de la función. Ejemplos.
Continuidad de una función en un punto
Video tutorial de matematicasbachiller.com
Tipos de discontinuidades
Video tutorial de matematicasbachiller.com
Ejemplos: Discontinuidad evitable
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Ejemplos: Discontinuidad de primera especie
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Ejemplos: Criterios de continuidad
40 ejemplos del estudio de la continuidad de una función.
21 ejemplos del estudio de la continuidad de una función.
17 ejemplos del estudio de la continuidad de una función.
4 ejemplos del estudio de la continuidad de una función.
4 ejemplos del estudio de la continuidad de una función.
4 ejemplos del estudio de la continuidad de una función.
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com

