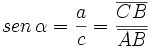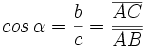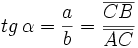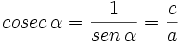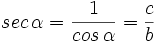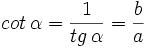Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Razones trigonométricas
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo  , de la siguiente manera: , de la siguiente manera:
|
Razones trigonométricas recíprocas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón recíproca del seno:
- La secante (abreviado como sec), razón recíproca del coseno:
- La cotangente (abreviado como cot), razón recíproca de la tangente:
|
Actividad interactiva: Razones trigonométricas
Actividad 1: Practica con las razones trigonométricas y ponte a prueba con una autoevaluación
Actividad:
|
Relaciones fundamentales de la trigonometría
{{Teorema|titulo=Relaciones fundamentales de la trigonometría
|enunciado=- 1.
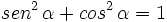
- 2.

- 3. {{Sube|porcentaje=+20%|contenido=
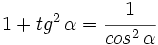 }
}
|demo=
1. 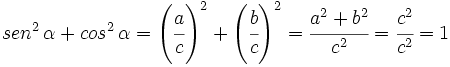
ya que, por el teorema de Pitágoras, 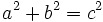 .
.
2. 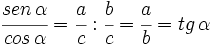
3. 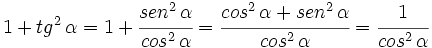
donde en el último paso hemos utilizado la primera relación fundamental: 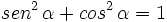 }
}