Fibonacci

De Wikipedia

Revisión de fecha 17:08 14 sep 2016; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Leonardo de Pisa (Fibonacci)

Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo (c. 1170 - 1250), también llamado Fibonacci, fue un matemático italiano, famoso por haber difundido en Europa el sistema de numeración actualmente utilizado, el que emplea notación posicional (de base 10, o decimal) y un dígito de valor nulo: el cero; y por idear la sucesión de Fibonacci (surgida como consecuencia del estudio del crecimiento de las poblaciones de conejos).

Tabla de contenidos

1 Vida
2 Obra
- 2.1 Liber Abaci
- 2.2 Liber Quadratorum
3 Video

[editar]

Vida

Estatua de Fibonacci en el Camposanto de Pisa

El apodo de Guglielmo (Guillermo), padre de Leonardo, era Bonacci (simple o bien intencionado). Leonardo recibió póstumamente el apodo de Fibonacci ( por filius Bonacci, hijo de Bonacci). Guglielmo dirigía un puesto de comercio en Bugía (según algunas versiones era el cónsul de Pisa), en el norte de África (hoy Bejaia, Argelia), y de niño Leonardo viajo allí para ayudarlo. Allí aprendió el sistema de numeración árabe.

Consciente de la superioridad y simplicidad sistema de numeración árabe-hindú frente al romano, Fibonacci viajó a través de los países del Mediterráneo para estudiar con los matemáticos árabes más destacados de ese tiempo, regresando cerca de 1200.

Leonardo fue huésped del Emperador Federico II que se interesaba en las matemáticas y la ciencia en general. En 1240, la República de Pisa lo honra concediéndole un salario permanente (bajo su nombre alternativo de Leonardo Bigollo).

En el siglo XIX, una estatua de Fibonacci fue construida y erigida en Pisa. Hoy en día, está situada en la galería oeste del Camposanto, cementerio histórico de la Piazza dei Miracoli.

[editar]

Obra

[editar]

Liber Abaci

En 1202, a los 32 años de edad, publicó lo que había aprendido en el Liber Abaci (libro del ábaco o libro de los cálculos). Este libro mostró la importancia del nuevo sistema de numeración árabe-hindú, aplicándolo a la contabilidad comercial, conversión de pesos y medidas, cálculo, intereses, cambio de moneda, y otras numerosas aplicaciones. En estas páginas describe el cero, la notación posicional, la descomposición en factores primos, los criterios de divisibilidad. El libro fue recibido con entusiasmo en la Europa ilustrada y tuvo un impacto profundo en el pensamiento matemático europeo.

Liber Abaci también plantea, y resuelve, un problema que implica el crecimiento de una hipotética población de conejos. La solución, generación por generación, fue una secuencia de números más tarde conocida como los números de Fibonacci. Esta secuencia ya era conocida por los matemáticos hindues del siglo VI, pero fue el Liber Abaci de Fibonacci quien la presentó al mundo occidental.

En la sucesión de Fibonacci, cada número (después de los dos primeros que son 1) es la suma de los dos números anteriores. La secuencia es:

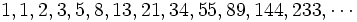
$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, \cdots$

Si dividimos cada número entre el siguiente, obtenemos una sucesión que se aproxima al llamado número de oro (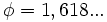 $\phi=1,618...\;$ )

[editar]

Liber Quadratorum

En el año 1225 publica su segundo y principal libro:"Liber Quadratorum", El Libro de los Números cuadrados, a raíz de un desafío de un matemático de la corte de Federico II que le propuso encontrar un cuadrado tal que si se le sumaba o restaba el número cinco diera como resultado en ambos casos números cuadrados.

Fibonacci comienza con los rudimentos de lo que se conocía de los números cuadrados desde la antigua Grecia y avanza gradualmente resolviendo proposiciones hasta dar solución al problema de análisis indeterminado que le habían lanzado como desafío.

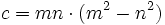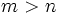En la parte original de la obra introduce unos números que denomina "congruentes" y que define, en terminología actual, como $c=mn \cdot(m^2-n^2)$ , donde $m\;$ y $n\;$ son enteros positivos impares, $m > n\;$ . De esta forma, el menor de ellos es 24. Enuncia y muestra que el producto de un número congruente por un cuadrado es otro número congruente.

Utiliza estos números como herramientas para sus posteriores proposiciones y los hace intervenir en una identidad que es conocida como "Identidad de Fibonacci". La identidad es:

$[\cfrac{1}{2}(m^2+n^2)]^2 \pm mn(m^2 - n^2) = [\cfrac{1}{2}(m^2 - n^2) \pm mn]^2$

Esta permite pasar con facilidad de un triángulo rectángulo a otro.

Leonardo de Pisa utiliza frecuentemente las proposiciones precedentes como lemas para las siguientes, por lo que el libro lleva un encadenamiento lógico. Sus demostraciones son del tipo retórico y usa segmentos de recta como representación de cantidades. Algunas proposiciones no están rigurosamente demostradas, sino que hace una especie de inducción incompleta, dando ejemplos prácticos y específicos, pero su dominio algorítmico es excelente y todo lo que afirma puede ser demostrado con las herramientas actuales. No se encuentran errores importantes si se hace excepción de la incompletitud de algunas demostraciones. El contenido del libro supera a la respuesta al desafío recibido y muestra el estado de la matemática de su época.

Desgraciadamente el manuscrito está incompleto y un interesante problema queda truncado. Pero el Liber Quadratorum es una de las obras fundamentales del saber humano y de las que honran a la humanidad. Ha sido traducida a muchos idiomas.

[editar]

Video

Fibonacci: La magia de los números (16') Sinopsis:

Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.

Fibonacci (24'29") Sinopsis: