Potencia de un punto respecto de una circunferencia (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Potencia de un punto a una circunferencia
Se llama potencia del punto
Observa que la potencia de 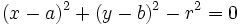 |
Proposición
Sea 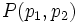 un punto del plano y una circunferencia
un punto del plano y una circunferencia 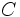 . Sean
. Sean 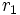 úna recta que corta a C en dos puntos:
úna recta que corta a C en dos puntos: 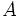 y
y 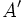 y sea
y sea 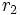 otra recta que corta a
otra recta que corta a 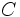 en otros dos puntos:
en otros dos puntos: 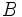 y
y 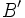 . Entonces se cumple que:
. Entonces se cumple que:
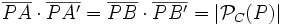
En la siguiente figura se puede observar que los triángulos 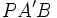 y
y  son semejantes porque tienen un ángulo común, el ángulo en
son semejantes porque tienen un ángulo común, el ángulo en  , y dos ángulos iguales, los ángulos en
, y dos ángulos iguales, los ángulos en 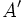 y en
y en 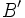 , por ser ángulos inscritos en la circunferencia que abarcan el mismo arco
, por ser ángulos inscritos en la circunferencia que abarcan el mismo arco  .
.
Por tanto, sus lados son proporcionales:
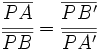
De donde, multiplicando en cruz:
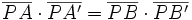
Para el caso en que l punto P pertenezca a la circunferencia:
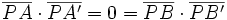
Veamos ahora que también es igual a 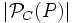 . Para ello vamos a considerar el siguiente gráfico, en el cual hemos tomado una recta r que pase por el centro de C y que la corta en dos puntos A y A', diametralmente opuestos:
. Para ello vamos a considerar el siguiente gráfico, en el cual hemos tomado una recta r que pase por el centro de C y que la corta en dos puntos A y A', diametralmente opuestos:
Se tiene que:
- Si P es exterior:
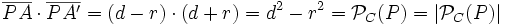 porque la potencia de un punto exterior es positiva.
porque la potencia de un punto exterior es positiva.
- Si P es interior:
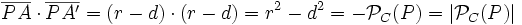 porque la potencia de un punto interior es negativa.
porque la potencia de un punto interior es negativa.
- Si P pertenece a la circunferencia:
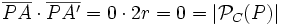 porque la potencia de un punto de la circunferencia es cero.
porque la potencia de un punto de la circunferencia es cero.
Ejemplo: Potencia de un punto respecto a una circunferencia
Calcula la potencia del punto P(6,4) respecto de la circunferencia de centro O(0,0) y radio r=3.
Calcula en tu cuaderno cuanto vale la potencia de ese punto respecto a la circunferencia y comprueba los resultados en la escena.
Hazlo tú:
- Calcula la potencia del punto P(-1,1) respecto de la circunferencia de centro O(-2,3) y radio 4.
- Calcula la potencia del punto P(0,7) respecto de la circunferencia de centro O(0,2) y radio 5.
Posición relativa de un punto respecto de una circunferencia
Dada una circunferencia de centro
En el dibujo de la derecha: A es exterior, B pertenece y C es interior a la circunferencia. |
Proposición
Dada una circunferencia 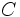 y un punto
y un punto  del plano:
del plano:
- Si el punto es exterior a la circunferencia:
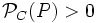
- Si el punto pertenece a la circunferencia:
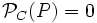
- Si el punto es interior a la circunferencia:
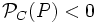
En efecto,
- Si P es exterior a C
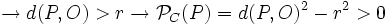
- Si P pertenece a C
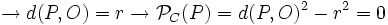
- Si P es interior a C
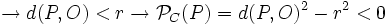
Ejemplo: Posición relativa de un punto respecto a una circunferencia
Halla la posición relativa del punto 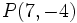 respecto a la circunferencia
respecto a la circunferencia  .
.
Calculemos la potencia de 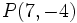 respecto a la circunferencia
respecto a la circunferencia  :
:
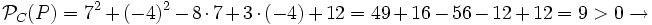 P es exterior a C.
P es exterior a C.
Eje radical de dos circunferencias
Se llama eje radical de dos circunferencias al lugar geométrico de los puntos del plano que tienen la misma potencia respecto a ambas circunferencias.
Ejemplo: Eje radical de dos circunferencias
- Halla el eje radical de las circunferencias:
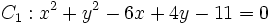
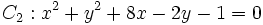 .
.
Igualando la potencia de un punto genérico 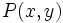 respecto a cada circunferencia, tenemos:
respecto a cada circunferencia, tenemos:
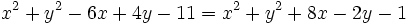
Simplificando las potencias al cuadrado y reagrupando términos:
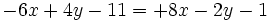
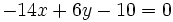
Proposición
El eje radical de dos circunferencias no concéntricas es una recta perpendicular a la recta determinada por los dos centros de las circunferencias.
Dadas las circunferencias de ecuaciones:
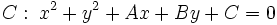
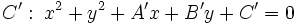 ,
,
con 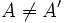 y/o
y/o 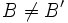 , para que no sean concéntricas.
, para que no sean concéntricas.
Su eje radical se obtiene igualando los miembros de la izquierda de cada ecuación:
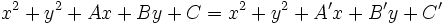
Simplificando los términos al cuadrado y pasando todos los términos al lado izquierdo de la ecuación, tenemos:

que es la ecuación implícita de una recta con vector normal 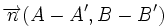 .
.
La recta que une los EscribeaquunafrmulacEscribeaquunafrmulaentros  y
y 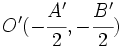 de las circunferencias, tiene vector director
de las circunferencias, tiene vector director
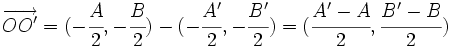
que es paralelo al vector normal del eje radical  .
.
Por tanto, el vector 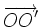 es perpendicular al eje radical.
es perpendicular al eje radical.
Dadas dos circunferencias concéntricas, como 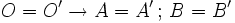 , entonces sus ecuaciones serán:
, entonces sus ecuaciones serán:
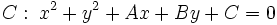
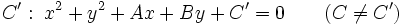 ,
,
su eje radical se obtiene igualando los miembros de la izquierda de cada ecuación:
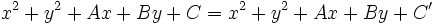
Simplificando los términos al cuadrado y pasando todos los términos al lado izquierdo de la ecuación, tenemos:

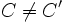 , y por tanto no tiene solución.
, y por tanto no tiene solución.Construcción geométrica del eje radical
Construcción geométrica del eje radical
- Si las circunferencias son exteriores, el eje radical se puede determinar trazando una perpendicular que pase por el punto medio (M en la figura) del segmento determinado por los puntos de contacto de la tangente a las circunferencias (puntos T1 y T2 en la figura).
- Si las circunferencias son tangentes, el eje radical contiene el punto de intersección de ambas circunferencias y es perpendicular a la recta determinada por los centros de las circunferencias.
- Si las circunferencias son secantes, el eje radical contiene los puntos de intersección de las circunferencias, puesto que ambos tienen potencia nula respecto de las circunferencias.
- Si una de las circunferencias es interior, se puede obtener el eje radical trazando una circunferencia auxiliar secante a las circunferencias dadas (a en la figura). El punto de intersección de los ejes radicales auxiliares (C en la figura) tiene igual potencia respecto a las circunferencias dadas, por tanto, el eje radical será la recta que contiene al punto C y es perpendicular a la recta determinada por los centros de las circunferencias iniciales. (Se debe elegir la circunferencia auxiliar de tal forma que los ejes radicales auxiliares se corten dentro del papel del dibujo).
|
Actividad interactiva: Eje radical de dos circunferencias
En la siguiente escena puedes ver como es el eje radical de dos circunferencias.
Actividad: Obtén el eje radical en los casos de circunferencias secantes, tangentes, exteriores o interiores. Varía los valores de los parámetros y observa cómo es el eje radical en cada caso.
|
Centro radical de tres circunferencias
Centro radical de tres circunferencias es el punto del plano que tiene igual potencia respecto de las tres circunferencias. Cálculo del centro radical de tres circunferencias Para determinar el eje radical de tres circunferencias, se halla la intersección del eje radical de una pareja de circunferencias con el eje radical de otro par de circunferencias. Demostración: Sean Como  tiene la misma potencia respecto a las tres circunferencias. tiene la misma potencia respecto a las tres circunferencias. |
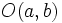 y radio
y radio  al número
al número
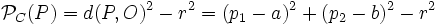
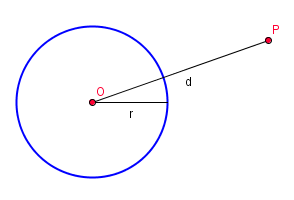


 y radio
y radio 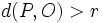
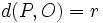
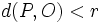
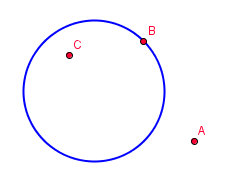

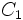 ,
, 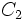 y
y 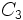 las tres circunferencias, y seaea
las tres circunferencias, y seaea 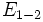 (eje radical de
(eje radical de 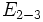 (eje radical de
(eje radical de 

