Utilidad de las funciones matemáticas
De Wikipedia
← Revisión anterior | Revisión siguiente →
Tabla de contenidos |
La función de proporcionalidad directa
Dos variables,  e
e  , son directamente proporcionales si el cociente entre ambas es constante:
, son directamente proporcionales si el cociente entre ambas es constante: 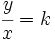
El saber o darse cuenta que entre dos variables existe proporcionalidad le ha permitido a multiples científicos desarrollar importantes leyes que se utilizan mucho en el campo de la física, de las cuales citaremos algunas.
La ley de elasticidad de Hooke
| La ley de Hooke que establece que la fuerza es directamente propocional a la distancia de compresión o estiramiento a que es sometido un resorte.
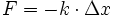
donde:
|
La segunda ley de Newton o ley fundamental de la dinámica
| Otra importante ley es la desarrollada por Isaac Newton conocida como la segunda ley de Newton que establece que la fuerza que actúa sobre un objecto tiene proporcionalidad directa con su aceleración, que matemáticamente se expresa así:
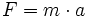
Como se puede ver en la segunda ley de Newton la constante de proporcionalidad es |
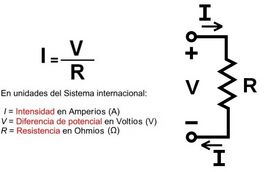
La ley de Ohm
La ley de Ohm, postulada por el físico y matemático alemán Georg Simon Ohm, es una ley de la electricidad. Establece que la diferencia de potencial 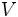 que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente 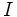 que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica 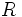 , que es el factor de proporcionalidad que aparece en la relación entre , que es el factor de proporcionalidad que aparece en la relación entre 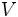 e e 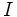 : :
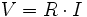
La fórmula anterior se conoce como Fórmula General de la Ley de Ohms, y en la misma, |
La función de proporcionalidad inversa
Dos variables, x e y, son inversamente proporcionales si el resultado de multiplicar ambas variables es constante: 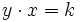 .
.
En el campo de la física hay muchos ejemplos de como importantes fórmulas enuncian de manera ejemplificante el concepto de lo que es una proporcionalidad inversa. Vamos a citar algunas de ellas.
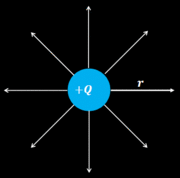
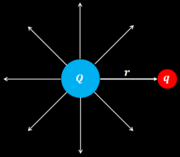
El potencial eléctrico
En el cálculo del potencial eléctrico 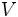 que genera una carga que genera una carga 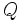 en funcíon de una distancia en funcíon de una distancia  , ambas variables tienen una relación de proporcionalidad inversa: , ambas variables tienen una relación de proporcionalidad inversa:
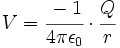 donde la constante de proporcionalidad es: 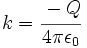 |
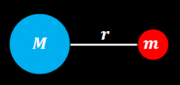
La energía potencial gravitatoria
Otro ejemplo de fórmula que utiliza el concepto de lo que es una proporcionalidad inversa es la fórmula que se utiliza para calcular la energía potencial gravitatoria cuándo la distancia entre las masas 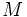 y y  es demasiado grande para considerar la aceleración de gravedad constante e igual g = 9.8m/s2 . es demasiado grande para considerar la aceleración de gravedad constante e igual g = 9.8m/s2 .
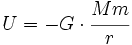 donde la constante de proporcionalidad es: 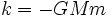 |
Energía potencial eléctrica
Otro ejemplo es la energía potencial eléctrica que se genera cuando una carga 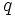 se mueve con respecto a otra carga puntual, se mueve con respecto a otra carga puntual, 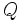 . Esta fórmula tiene una relación de proporcionalidad inversa: . Esta fórmula tiene una relación de proporcionalidad inversa:
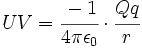 En donde la constante de proporcionalidad es: 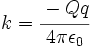 |
La función cuadrática
En el mundo de la física existen variadas fórmulas que se rigen mediante funciones cuadráticas, especialmente del tipo 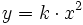 . Veamos algunas de ellas.
. Veamos algunas de ellas.
Energía cinética
En el cálculo de la energía cinética 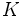 de un cuerpo de masa de un cuerpo de masa  que se desplaza a una velocidad que se desplaza a una velocidad 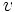 , la variable , la variable 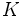 y la variable y la variable 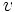 tienen una relación de éste tipo: tienen una relación de éste tipo:
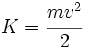 |
Energía potencial elástica
Otra fórmula que se utiliza mucho en los cáculos físicos es la energía potencial elástica 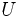 de un resorte que se comprime o se estira hasta una distancia de un resorte que se comprime o se estira hasta una distancia  especifica: especifica:
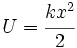 |
Potencia eléctrica
Otra fórmula bien usada es la que establece que la potencia elétrica disipada 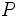 en función de la corriente eléctrica en función de la corriente eléctrica 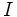 que fluye por un segmento de un alambre eléctrico, en donde la potencia eléctrica que fluye por un segmento de un alambre eléctrico, en donde la potencia eléctrica 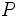 es directamente proporcional al cuadrado de es directamente proporcional al cuadrado de 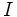 : :
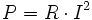 |
La función irracional
Veamos una aplicación de la función irracional en el campo de la física:
El péndulo simple
Un péndulo simple es uno tal, que se puede considerar como una masa puntual, suspendida de una cuerda o varilla de masa despreciable.
Para pequeñas amplitudes, el periodo 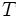 de tal péndulo, se puede aproximar por:
de tal péndulo, se puede aproximar por:
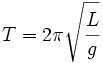
siendo:
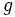 : aceleración de la gravedad terrestre.
: aceleración de la gravedad terrestre.
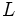 : longitud del péndulo.
: longitud del péndulo.
Sean Carroll relata la historia del descubrimiento de Galileo sobre el hecho de que para pequeñas amplitudes, el período y la frecuencia no se ven afectados por la amplitud. "Según se informa, en 1581, un joven Galileo Galilei hizo un descubrimiento revolucionario mientras estaba sentado y aburrido durante un servicio religioso en una iglesia de Pisa. La araña que pendia del techo sobre su cabeza, oscilaba suavemente hacia atrás y hacia delante, pero parecia moverse más rápidamente cuando el balanceo era más amplio (por ejemplo, después de una ráfaga de viento), y más lentamente cuando el balanceo era más corto. Intrigado, Galileo decidió medir el tiempo que duraba cada oscilación, utilizando para ello el único evento aproximadamente periódico al que tenia fácil acceso: los latidos de su propio pulso. Encontró algo interesante: el número de latidos del corazón entre los vaivenes de la araña era más o menos el mismo, independientemente de si las oscilaciones eran anchas o estrechas. El tamaño de las oscilaciones - la amplitud del recorrido del péndulo hacia adelante y hacia atrás-, no afectaba a la frecuencia de estas oscilaciones.
La función logarítmica
Veamos algunas aplicaciones de la función logarítmica en la vida real:
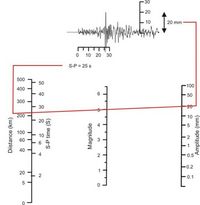
Escala de Richter
La escala sismológica de Richter, también conocida como escala de magnitud local (ML), es una escala logarítmica arbitraria que asigna un número para cuantificar la energía que libera un terremoto, denominada así en honor del sismólogo estadounidense Charles Francis Richter (1900-1985).
La sismología mundial usa esta escala para determinar la fuerza de seismos de una magnitud entre 2,0 y 6,9 y de 0 a 400 kilómetros de profundidad. Aunque los medios de comunicación suelen confundir las escalas, para referirse a eventos telúricos actuales se considera incorrecto decir que un seismo «fue de magnitud superior a 7,0 en la escala de Richter», pues los seismos con magnitud superior a 6,9 se miden desde 1978 con la escala sismológica de magnitud de momento, por tratarse esta última de una escala que discrimina mejor en los valores extremos.
Fue desarrollada por Charles Francis Richter con la colaboración de Beno Gutenberg en 1935, ambos investigadores del Instituto de Tecnología de California, con el propósito original de separar el gran número de terremotos pequeños de los menos frecuentes terremotos mayores observados en California en su tiempo. La escala fue desarrollada para estudiar únicamente aquellos terremotos ocurridos dentro de un área particular del sur de California cuyos sismogramas hubieran sido recogidos exclusivamente por el sismómetro de torsión de Wood-Anderson.
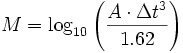
donde:
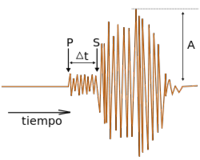
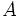 = amplitud de las ondas en milímetros, tomada directamente en el sismograma.
= amplitud de las ondas en milímetros, tomada directamente en el sismograma.
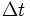 = tiempo en segundos desde el inicio de las ondas P (Primarias) al de las ondas S (Secundarias).
= tiempo en segundos desde el inicio de las ondas P (Primarias) al de las ondas S (Secundarias).
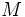 = magnitud arbitraria pero constante a terremotos que liberan la misma cantidad de energía.
= magnitud arbitraria pero constante a terremotos que liberan la misma cantidad de energía.
El uso del logaritmo en la escala es para reflejar la energía que se desprende en un terremoto. Una escala logarítmica hace que los valores asignados a cada nivel aumenten de forma logarítmica, y no de forma lineal. Esto significa que un terremoto de magnitud 6 es 10 veces más potente que uno de magnitud 5. Richter tomó la idea del uso de logaritmos en la escala de magnitud estelar, usada en astronomía para describir el brillo de las estrellas y de otros objetos celestes.
Magnitud aparente de un objeto celeste
La magnitud aparente (m) de un objeto celeste es un número que indica la medida de su brillo tal y como es visto por un observador desde la Tierra y la cantidad de luz (energía) que se recibe del objeto. Mientras que la cantidad de luz recibida depende realmente del ancho de la atmósfera, las magnitudes aparentes se normalizan a un valor que tendrían fuera de la atmósfera. Cuanto menor sea el número, más brillante aparece una estrella. El Sol, con magnitud aparente de −27, es el objeto más brillante en el cielo. Se ajusta al valor que tendría en ausencia de la atmósfera. Cuanto más brillante aparece un objeto, menor es su valor de magnitud (es decir, la relación inversa). Además, la escala de magnitudes es logarítmica: una diferencia de una magnitud corresponde a un cambio en el brillo de un factor alrededor de 2,512.
Generalmente, se utiliza el espectro visible (vmag) como base para la magnitud aparente. Sin embargo, se utilizan también otros espectros (por ejemplo, la banda J del infrarrojo cercano). En el espectro visible, Sirio es la estrella más brillante después del Sol. En la banda-J del infrarrojo cercano, Betelgeuse es la más brillante. La magnitud aparente de las estrellas se mide con un bolómetro.
La magnitud aparente puede medirse para determinadas bandas del espectro luminoso. En el caso del espectro visible, se denomina magnitud visual (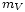 ) y puede ser estimada por el ojo humano.
) y puede ser estimada por el ojo humano.
Actualmente se utilizan los fotómetros que permiten medir magnitudes con mucha precisión. Éste es capaz de catalogar en orden de magnitud aparente y distinguir cuando dos estrellas tienen la misma magnitud aparente o una estrella y una fuente artificial.
La escala con la que se mide la magnitud, tiene su origen en la práctica helenística de dividir las estrellas visibles con ojo desnudo en seis magnitudes. Las estrellas más visibles a simple vista fueron pensadas para formar parte de la primera magnitud (m = +1), mientras que las más débiles eran consideradas como sexta magnitud (m = +6), el límite del ojo humano (sin ayuda de un telescopio). Este método, algo primitivo, para indicar la visibilidad de las estrellas a simple vista fue divulgado por Ptolomeo en su Almagesto, y se cree que pudo haber sido originado por Hiparco de Nicea. Este sistema original no medía la magnitud del Sol. Debido al hecho de que la respuesta del ojo humano a la luz es logarítmica la escala que resulta es también logarítmica.
En 1856 Norman Pogson formalizó el sistema definiendo que una típica estrella de primera magnitud es aquella 100 veces más visible que una típica estrella de magnitud sexta; así, una estrella de primera magnitud es aproximadamente 2.512 veces más visible que una de segunda magnitud. La raíz quinta de 100, aprox. 2.512, se conoce como cociente de Pogson. La escala de Pogson se fijó originalmente asignando a la estrella Polaris la magnitud de 2. Pero dado que los astrónomos han descubierto que la estrella polar es levemente variable, ahora se utiliza la estrella Vega como referencia.
El sistema moderno no se limita a 6 magnitudes. Los objetos realmente visibles tienen magnitudes negativas. Por ejemplo Sirius, la estrella más visible, tiene una magnitud aparente de -1.44 a -1.46. La escala moderna incluye a la Luna y al Sol; la Luna tiene una magnitud aparente de -12.6 y el Sol tiene una magnitud aparente de -26.7. Los telescopios Hubble y Keck han localizado estrellas con magnitudes de +30.
La magnitud aparente en la banda x se puede definir como:
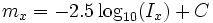
donde 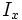 es el flujo luminoso observado en la banda
es el flujo luminoso observado en la banda  , y
, y 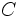 es una constante que depende de las unidades de flujo y de la banda.
es una constante que depende de las unidades de flujo y de la banda.
La función exponencial
Veamos algunas aplicaciones de la función exponencial en la vida real:
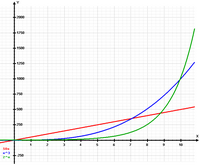
Fenómenos que crecen de forma exponencial
El crecimiento exponencial
La expresión crecimiento exponencial se aplica a una magnitud tal que varía en el tiempo de acuerdo a la ecuación: 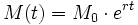
[editar] El modelo exponencialUn caso particular de crecimiento exponencial es el llamado modelo exponencial: El modelo exponencial es un modelo demográfico y ecológico para representar el crecimiento de las poblaciones y la difusión epidémica de un rasgo entre una población, basado en el crecimiento exponencial. Su ecuación es como la del crecicmiento exponencial 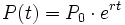 donde |
Algunos fenómenos que pueden ser descritos por un crecimiento exponencial, al menos durante un cierto intervalo de tiempo, son:
- El número de células de un embrión mientras se desarrolla en el útero materno.
- En una economía sin trastornos, los precios crecen exponencialmente, donde la tasa coincide con el índice de inflación.
- El crecicmiento de un capital a interés compuesto en un periodo de tiempo con amortizaciones periódicas.
- El crecicmiento de un capital a interés continuo (interés compuesto con amortizaciones instantáneas) en un periodo de tiempo.
- El número de contraseñas posibles con n dígitos crece exponencialmente con n.
- El número de bacterias que se reproducen por fisión binaria.
- El número de miembros en poblaciones de ecosistemas cuando carecen de predador y los recursos son ilimitados (no existe competencia intraespecífica).
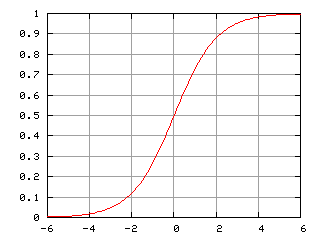
La función logística
La función logística, curva logística o curva en forma de S es una función matemática que aparece en diversos modelos de crecimiento de poblaciones, propagación de enfermedades epidémicas y difusión en redes sociales. Dicha función constituye un refinamiento del modelo exponencial para el crecimiento de una magnitud. Su gráfica pertenece al conjunto de las funciones sigmoideas.
El estudio inicial de crecimiento es aproximadamente exponencial; al cabo de un tiempo, aparece la competencia entre algunos miembros de la población por algún recurso crítico y la tasa de crecimiento disminuye; finalmente, en la madurez, el crecimiento se detiene.
La función logística simple se define mediante la expresión matemática:
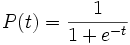
donde la variable P puede ser considerada o denotada como población, donde e es la constante de Euler (númerto e) y la variable t puede ser considerada el tiempo.
En su forma más general, la función logística se define por la fórmula matemática:
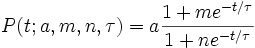
para parámetros reales a, m, n, y τ. Estas funciones tienen un campo de aplicación muy amplio, desde la biología a la economía.
Como ejemplo tenemos el desarrollo embrionario. En el desarrollo de un embrión, el óvulo fecundado comienza a dividirse y el número de células empieza a crecer: 1, 2, 4, 8, 16, 32, 64, etc. Éste es un crecimiento exponencial. Pero el feto sólo puede crecer hasta un tamaño que el útero pueda soportar; así, otros factores comienzan a disminuir el incremento del número de células, y la tasa de crecimiento disminuye. Después de un tiempo, el niño nace y continúa creciendo. Finalmente, el número de células se estabiliza y la estatura del individuo se hace constante. Se ha alcanzado la madurez, en la que el crecimiento se detiene.
La ecuación Verhulst y la catástrofe malthusiana
Una típica aplicación de la ecuación logística es un modelo común del crecimiento poblacional según el cual:
- La tasa de reproducción es proporcional a la población existente.
- La tasa de reproducción es proporcional a la cantidad de recursos disponibles.
El segundo término modela, por tanto, la competición por los recursos disponibles, que tiende a limitar el crecimiento poblacional.
Su ecuación viene dada por:
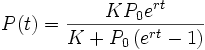
donde la constante 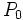 es la población inicial, la constante
es la población inicial, la constante  define la tasa de crecimiento y
define la tasa de crecimiento y 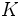 es la capacidad de persistencia o capacidad de carga. La capacidad de carga de una especie biológica en un ambiente es el tamaño máximo de población que el ambiente puede soportar indefinidamente en un periodo determinado, teniendo en cuenta el alimento, agua, hábitat, y otros elementos necesarios disponibles en ese ambiente.
es la capacidad de persistencia o capacidad de carga. La capacidad de carga de una especie biológica en un ambiente es el tamaño máximo de población que el ambiente puede soportar indefinidamente en un periodo determinado, teniendo en cuenta el alimento, agua, hábitat, y otros elementos necesarios disponibles en ese ambiente.
La ecuación Verhulst fue publicada por primera vez por Pierre François Verhulst en 1838 después de haber leído el "Ensayo sobre el principio de población" del demógrafo y economista político conservador Thomas Malthus. En este ensayo Malthus expone lo que se pasará a conocer como "la catástrofe malthusiana", una visión pesimista del crecimiento de población. Las tesis de Malthus aunque desajustadas a los hechos, tuvieron gran influencia política. Malthus llegó a afirmar que el crecimiento de la población libre de contenciones era un crecimiento exponencial, mientras que la producción de alimentos según su argumento era un crecimiento lineal. Puesto que la tasa de crecimiento de la población era más acelerada que la de alimentos a partir de un cierto umbral de población, Malthus pronosticó que habría una escasez de alimentos y una gran hambruna hacia mediados del siglo XIX. La gran hambruna predicha por Malthus jamás se produjo mostrando que los presupuestos lógicos de Malthus eran simplistas y en ocasiones hasta erróneos.
Fenómenos que decrecen de forma exponencial
También es de interés físico el decrecimiento exponencial, por el cual una cierta magnitud 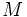 con el tiempo disminuye su valor, o se "atenúa" según una ley exponencial negativa del tipo:
con el tiempo disminuye su valor, o se "atenúa" según una ley exponencial negativa del tipo:
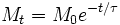
Algunos fenómenos que siguen procesos de decrecimiento o atenuación exponencial son:
- La velocidad de un pequeño objeto sobre el que no actúan fuerzas en el seno de un fluido en reposo.
- La intensidad de corriente en un circuito eléctrico de continua con inductancia nula al que se le retira la tensión eléctrica.
- El número de átomos de una substancia radioactiva que se desintegran por unidad de tiempo.
- La intensidad luminosa de un haz de luz que se propaga en un medio absorbente.
- La probabilidad de supervivencia de ciertas especies que no muestran envejecimiento celular genéticamente determinado como muchos reptiles.
- El coeficiente de influencia en las sinapsis neuronales, lo cual explica el olvido a largo plazo.
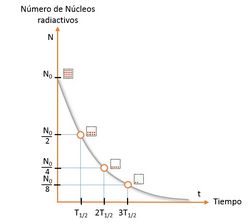
Desintegración radioactiva
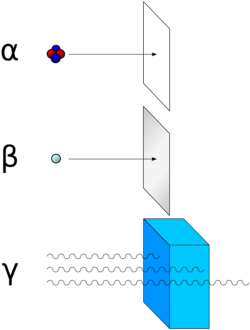
Las partículas alfa (núcleos de helio) se detienen al interponer una hoja de papel. Las partículas beta (electrones y positrones) no pueden atravesar una capa de aluminio. Sin embargo, los rayos gamma (fotones de alta energía) necesitan una barrera mucho más gruesa, y los más energéticos pueden atravesar el plomo.
La radiactividad o radioactividad es un fenómeno físico por el cual los núcleos de algunos elementos químicos, llamados radiactivos, emiten radiaciones que tienen la propiedad de impresionar placas radiográficas, ionizar gases, producir fluorescencia, atravesar cuerpos opacos a la luz ordinaria, entre otros. Debido a esa capacidad, se les suele denominar radiaciones ionizantes (en contraste con las no ionizantes). Las radiaciones emitidas pueden ser electromagnéticas, en forma de rayos X o rayos gamma, o bien corpusculares, como pueden ser núcleos de helio, electrones o positrones, protones u otras. En resumen, es un fenómeno que ocurre en los núcleos de ciertos elementos inestables, que son capaces de transformarse o decaer, espontáneamente, en núcleos atómicos de otros elementos más estables. Así un isótopo pesado puede terminar convirtiéndose en uno mucho más ligero, como el uranio que, con el transcurrir de los siglos, acaba convirtiéndose en plomo.
La radiactividad se aprovecha para la obtención de energía nuclear, se usa en medicina (radioterapia y radiodiagnóstico) y en aplicaciones industriales (medidas de espesores y densidades, entre otras).
En general son radiactivas las sustancias que no presentan un balance correcto entre protones o neutrones. Cuando el número de neutrones es excesivo o demasiado pequeño respecto al número de protones, se hace más difícil que la fuerza nuclear fuerte debido al efecto del intercambio de piones pueda mantenerlos unidos. Finalmente, el desequilibrio se corrige mediante la liberación del exceso de neutrones o protones, en forma de partículas α que son realmente núcleos de helio, y partículas β, que pueden ser electrones o positrones. Estas emisiones llevan a dos tipos de radiactividad:
- Radiación α, que aligera los núcleos atómicos en 4 unidades másicas, y cambia el número atómico en dos unidades.
- Radiación β, que no cambia la masa del núcleo, ya que implica la conversión de un protón en un neutrón o viceversa, y cambia el número atómico en una sola unidad (positiva o negativa, según si la partícula emitida es un electrón o un positrón).
Un tercer tipo de radiación, la radiación γ, se debe a que el núcleo pasa de un estado excitado de mayor energía a otro de menor energía, que puede seguir siendo inestable y dar lugar a la emisión de más radiación de tipo α, β o γ. La radiación γ es, por tanto, un tipo de radiación electromagnética muy penetrante, ya que tiene una alta energía por fotón emitido.
La desintegración radiactiva se comporta en función de la ley de decaimiento exponencial:
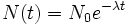
donde:
-
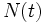 es el número de radioisótopos o radionúclidos existentes en un instante de tiempo t.
es el número de radioisótopos o radionúclidos existentes en un instante de tiempo t.
-
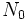 es el número de radioisótopos existentes en el instante inicial t = 0.
es el número de radioisótopos existentes en el instante inicial t = 0.
-
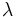 , llamada constante de desintegración radiactiva, es la probabilidad de desintegración por unidad de tiempo. La constante de desintegración es el cociente entre el número de desintegraciones por segundo y el número de átomos radiactivos (
, llamada constante de desintegración radiactiva, es la probabilidad de desintegración por unidad de tiempo. La constante de desintegración es el cociente entre el número de desintegraciones por segundo y el número de átomos radiactivos (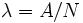 ).
).
Se llama tiempo de vida o tiempo de vida media de un radioisótopo el tiempo promedio de vida de un átomo radiactivo antes de desintegrarse. Es igual a la inversa de la constante de desintegración radiactiva ( ).
).
Al tiempo que transcurre hasta que la cantidad de núcleos radiactivos de un isótopo radiactivo se reduzca a la mitad de la cantidad inicial se le conoce como periodo de semidesintegración, período, semiperiodo, semivida o vida media (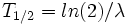 ). Al final de cada período, la radiactividad se reduce a la mitad de la radiactividad inicial. Cada radioisótopo tiene un semiperiodo característico, en general diferente del de otros isótopos.
). Al final de cada período, la radiactividad se reduce a la mitad de la radiactividad inicial. Cada radioisótopo tiene un semiperiodo característico, en general diferente del de otros isótopos.
El periodo de semidesintegración del uranio-238 es aproximadamente 4.470 millones de años y el del uranio-235 es 704 millones de años,3 lo que los convierte en útiles para estimar la edad de la Tierra.}
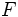 es el módulo de la fuerza que se aplica sobre el muelle.
es el módulo de la fuerza que se aplica sobre el muelle.
 es la constante elástica del muelle, que relaciona fuerza y alargamiento. Cuanto mayor es su valor más trabajo costará estirar el muelle. Depende del muelle, de tal forma que cada uno tendrá la suya propia.
es la constante elástica del muelle, que relaciona fuerza y alargamiento. Cuanto mayor es su valor más trabajo costará estirar el muelle. Depende del muelle, de tal forma que cada uno tendrá la suya propia.
 es la variación en longitud que sufre el muelle con respecto a sus estado de reposo.
es la variación en longitud que sufre el muelle con respecto a sus estado de reposo.
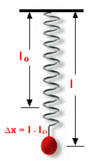
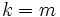 , que es la masa del objecto al que se le aplica la fuerza, y que se considera constante.
, que es la masa del objecto al que se le aplica la fuerza, y que se considera constante.
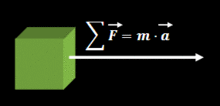
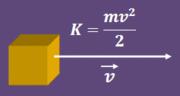
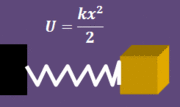
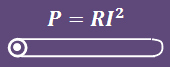
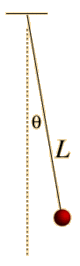

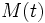 es valor de la magnitud en el instante
es valor de la magnitud en el instante 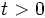 .
.
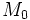 es el valor inicial de la variable, valor en
es el valor inicial de la variable, valor en 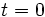 , cuando empezamos a medirla.
, cuando empezamos a medirla.
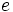 = 2,718281828459...
= 2,718281828459...
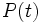 es el tamaño de la población en un instante t;
es el tamaño de la población en un instante t;