Plantilla:Crecimiento de una función en un intervalo (1ºBach)
De Wikipedia
Tasa de variación media
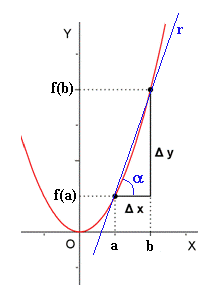
Para medir el crecimiento de una función en un intervalo [a,b], se utiliza la tasa de variación media (T.V.M.), que se define como el cociente de la variación de y entre la variación de x:
Si llamamos
|
Proposición
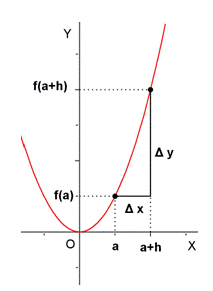
- La T.V.M. de una función en un intervalo [a,b] es igual a la pendiente de la recta secante a la gráfica de la función en puntos de abcisas a y b.
- Definición de T.V.M. de f en el intervalo [a,a+h]. Interpretación geométrica. Ejemplos
Algunos ejemplos que relacionan el concepto de tasa de variación media con el de velocidad media.
|
Actividad Interactiva: Tasa de variación media
Actividad 1: En esta escena calcularas la tasa de variación de una función en distintos intervalos.
Actividad: En la siguiente escena tienes representada una función (en blanco).
Observa como la T.V.M. y la pendiente de la recta secante (en celeste), en cada intervalo valen lo mismo. |
Ejemplos: Tasa de variación media
- Cálculo de la tasa de variación de las funciones:
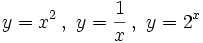 .
.
- Cálculo de la tasa de variación de la función:
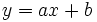 .
.
- Cálculo de la tasa de variación de la función:
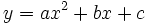 .
.
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(b)-f(a)}{b-a}](/wikipedia/images/math/8/9/c/89c85ce438b13f83f07e3480026d5be8.png)
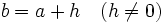 , la expresión anterior queda como sigue:
, la expresión anterior queda como sigue:
![T.V.M._f \,[a,a+h]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(a+h)-f(a)}{h}](/wikipedia/images/math/c/8/1/c81e647a1a3e3e683857d6714eed390f.png)
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=tg\, \alpha=m](/wikipedia/images/math/6/b/7/6b761a6a89fc5990f82ffd9ae6ec3b0e.png)
 es la pendiente de la recta r.
es la pendiente de la recta r.