Plantilla:Crecimiento de una función en un intervalo (1ºBach)
De Wikipedia
Tasa de variación media
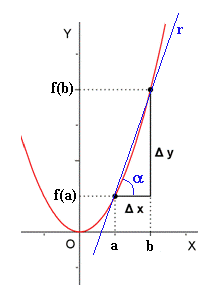
Para medir el crecimiento medio de una función en un intervalo [a,b], se utiliza la tasa de variación media (T.V.M.), que se define como el cociente de la variación de y entre la variación de x:
Si llamamos
En esta escena podrás ver calcular la T.V.M. de la función que tú quieras. |
Proposición
La T.V.M. de una función en un intervalo ![[a,b]\;](/wikipedia/images/math/9/a/e/9ae0a6959368a1b0c6be4a9feb1e9b5c.png) es igual a la pendiente de la recta secante a la gráfica de la función en puntos de abcisas
es igual a la pendiente de la recta secante a la gráfica de la función en puntos de abcisas  y
y  .
.
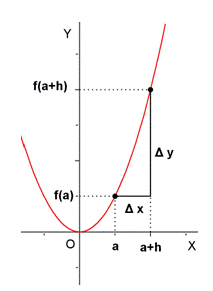
- Definición de T.V.M. de f en el intervalo [a,a+h]. Interpretación geométrica. Ejemplos
Algunos ejemplos que relacionan el concepto de tasa de variación media con el de velocidad media.
Ejemplos: Tasa de variación media
- En este vídeo jugamos con el concepto de "tasa de cambio" de una función en un intervalo.
Dicho concepto tendrá protagonismo estelar cuando hablemos de la "derivada" de una función en un punto.
- Cálculo de la tasa de variación de las funciones:
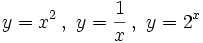 .
.
Como sabe todo el mundo, la tasa de cambio de la función "f" cuando la variable independiente varía desde "x" a "x+h" es (f(x+h) - f(x)/h.
Si f(x) = a·x + b (o sea, la gráfica de "f" es una recta), la tasa de cambio cuando la variable independiente varía desde "x" a "x+h" es "a".
Como sabe todo el mundo, la tasa de cambio de la función "f" cuando la variable independiente varía desde "x" a "x+h" es (f(x+h) - f(x)/h.
Si f(x) = a·x2+b·x+c (o sea, la gráfica de "f" es una parábola de eje vertical), la tasa de cambio cuando la variable independiente varía desde "x" a "x+h" es a·h+2·a·x+b. En el vídeo, además, interpretamos este resultado con un ejemplo de la vida cotidiana.
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(b)-f(a)}{b-a}](/wikipedia/images/math/8/9/c/89c85ce438b13f83f07e3480026d5be8.png)
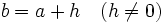 , la expresión anterior queda como sigue:
, la expresión anterior queda como sigue:
![T.V.M._f \,[a,a+h]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(a+h)-f(a)}{h}](/wikipedia/images/math/c/8/1/c81e647a1a3e3e683857d6714eed390f.png)
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=tg\, \alpha=m](/wikipedia/images/math/6/b/7/6b761a6a89fc5990f82ffd9ae6ec3b0e.png)
 es la pendiente de la recta r.
es la pendiente de la recta r.