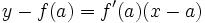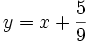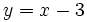Plantilla:Utilidad de la derivada (1ºBach)
De Wikipedia
Tabla de contenidos |
Cálculo de la ecuación de la recta tangente a una curva
Proposición
La ecuación de la recta tangente a la curva  en un punto de abscisa
en un punto de abscisa  viene dada por la ecuación:
viene dada por la ecuación:
|
|
Ejemplo: Ecuación de la recta tangente
Dada la función 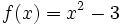 , halla la ecuación de la recta tangente en el punto
, halla la ecuación de la recta tangente en el punto 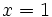 .
.
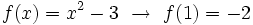
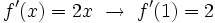
La ecuación de la recta tangente a la curva en el punto 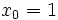 es:
es:
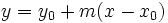
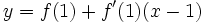
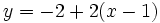
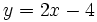
Puedes comprobar el resultado en la siguiente escena:
En esta escena podrás calcular la ecuación de la recta tangente a una curva .
Ejercicio resuelto: Ecuación de la recta tangente
Dada la función 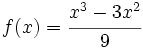 , halla las ecuaciones de la rectas tangentes que sean paralelas a la bisectriz del primer cuadrante</math>.
, halla las ecuaciones de la rectas tangentes que sean paralelas a la bisectriz del primer cuadrante</math>.
Hay dos soluciones:
Puedes comprobar el resultado en la siguiente escena:
En esta escena podrás calcular la ecuación de la recta tangente a una curva .
Estudio del crecimiento
Procedimiento
Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada:
- En aquellos puntos donde la derivada sea positiva la función será creciente.
- En aquellos puntos donde la derivada sea negativa la función será decreciente.
Estudio de los puntos singulares
Se llaman puntos singulares de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal.
Esos puntos pueden ser máximos o mínimos, pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función.
Problemas de optimización
Un problema de optimización es aquél en el que se pretende averiguar el máximo o el mínimo de una magnitud dada.
Por ejemplo, encontrar el área mínima, el menor coste, la forma óptima, la menor resistencia, el máximo beneficio, el mayor alcance...
Procedimiento
- Identifica todas las cantidades dadas y las cantidades a determinar.
- Escribe una ecuación primaria para la magnitud que debe hacerse máxima o mínima.
- Reduce la ecuación primaria a una ecuación que sólo tenga una variable independiente. Este paso te puede exigir el utilizar ecuaciones secundarias que relacionen las variables independientes de la ecuación primaria. (Las despejas en las secundarias y las sustituyes en la primaria)
- Fija el dominio de la ecuación primaria. Ésto es, determina el rango de valores para los que tiene sentido el problema planteado.
- Obtén el valor máximo o mínimo solicitado mediante el estudio de los ceros y del crecimiento de la función derivada.
- Introducción a los problemas de optimización.
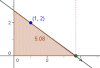
- Ejemplo 1: Hallar el punto de la parábola
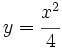 más próximo al punto (-1,2).
más próximo al punto (-1,2).
- Ejemplo 2: Hallar el punto de la curva
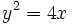 más próximo al punto (2,-1).
más próximo al punto (2,-1).
Actividades interactivas: Problemas de optimización
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar loa solución del problema.
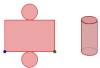
¿Cuáles serán las dimensiones de la lata más barata (en cuanto a superficie de hojalata)?.
Escena de Geogebra para visualizar la solución del problema.
Problema 4b: De todas las rectas que pasan por el punto (a,b), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
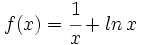 , determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente.
, determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente.
Escena de Geogebra para visualizar la solución del problema.
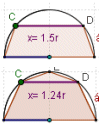
Problema 7b: En una semicircunferencia de diámetro AB=2r se traza una cuerda CD paralela a AB. Llamamos E al punto medio del arco CD y dibujamos el pentágono ACEDB. Calcula la longitud de la cuerda CD para que el área del pentágono sea máxima.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Problema 8b: Un nadador, A, se encuentra a 3 km de la playa en frente de una caseta (C). Desea ir a B, en la misma playa, a 6 km de la caseta. Sabiendo que nada a v1 km/h y corre por la arena a v2 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Aplicación al cálculo de límites: Regla de L'Hopital
Para ampliar
Calculo de la variación porcentual.