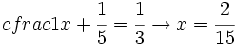Plantilla:Resolución de problemas mediante ecuaciones de primer grado
De Wikipedia
Procedimiento
Para resolver un problema mediante una ecuación hay que seguir los siguientes pasos:
- Determinar la incógnita.
- Traducir el enunciado del problema al lenguaje algebraico mediante una ecuación en la que intervenga la incógnita.
- Resolver la ecuación, es decir, hallar el valor de la incógnita.
- Dar la solución del problema a partir del valor obtenido de la incógnita.
Aquí tienes una colección de problemas con un nivel de dificultad bajo para que vayas cogiendo práctica.
Pulsa el botón EJEMPLO para ver más problemas.
Pulsa el botón DATOS para ver otro problema similar, pero con datos diferentes.
Ejercicios resueltos
- Un repostero ha mezclado 12 kg de azúcar de 1.10 €/kg con una cierta cantidad de miel de 4.20 €/kg para que la mezcla le salga a 2.34 €/kg. ¿Cuánta miel tuvo que poner?
- La distancia entre dos ciudades, A y B, es de 280 km. Untren sale de A hacia B a 80 km/h, y media hora más tarde sale un coche de B hacia A que tarda 1.2 horas en cruzarse con el tren. ¿Qué velocidad lleva el coche?
- Tres amigos trabajan 20, 30 y 50 días en un negocio. Al cabo de tres meses se reparten los beneficios y al tercero le corresponden 300 € más que al segundo. ¿Cuál es la cantidad repartida?
- Dos grifos llenan un depósito en 3 horas. Si sólo se abre uno de ellos, tardaría 5 horas. ¿Cuánto tardará el otro grifo en llenar el depósito?
Solución:
Solución 1:
x = kg de miel
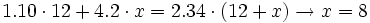 kg de miel
kg de miel
Solución 2:
x = velocidad del coche
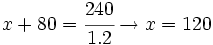 km/h
km/h
Solución 3:
x = beneficio del 1º
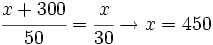 € corresponden al primero.
€ corresponden al primero.
y = beneficio del 2º
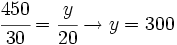 € corresponden al segundo.
€ corresponden al segundo.
La cantidad repartida es : 300+450+750=1500 €
Solución 4:
1/5 = fracción de depósito que llena uno de los grifos en 1 h
x = fracción de depósito que llena el otro grifo en 1 h