Plantilla:Representación de funciones polinómicas (1ºBach)
De Wikipedia
Procedimiento
En el estudio y representación gráfica de una función polinómica, f(x),tendremos que determinar los siguientes apartados:
- Dominio:
.
- Puntos de corte: Los puntos de corte con el eje X se obtienen resolviendo la ecuación f(x)=0, para lo que tendremos que resolver una ecuación polinómica usando las técnicas vistas en temas anteriores. El punto de corte con el eje Y se obtiene calculando f(0).
- Signo de f(x): para el estudio del signo usaremos sólo los puntos de corte ya que una función polinómica no tiene discontinuidades.
- Puntos singulares de f(x) que se obtienen resolviendo la ecuación f'(x)=0. Por tanto, tendremos que resolver otra ecuación polinómica.
- Intervalos de crecimiento y decrecimiento de f(x): a partir de los puntos singulares y estudiando el signo de f'(x). Así podremos determinar los máximos y mínimos relativos de f(x).
- Asíntotas y ramas infinitas: Las funciones polinómicas no tienen ningún tipo de asíntotas. Tan sólo habrá que estudiar el límite cuando x tiende a +/- infinito.
- Simetrías: ver si f(x) es par o impar.
Ejemplo 1: Ceros (4'49") Sinopsis: Los ceros de un polinomio son los puntos de corte de la función polinómica con el eje X.
En este ejemplo calcularemos los ceros del polinomio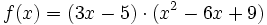 
Ejemplo 2: Crecimiento y extremos (9'54") Sinopsis: Crecicmiento y extremos de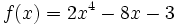 
Ejemplo 3: Representación gráfica (28'16") Sinopsis: Estudio y representación gráfica de la función polinómica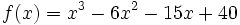 
Ejercicios resueltos: Estudio y representación gráfica de funciones polinómicas
Estudia y representa:
- a)
.
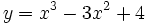- b)
.
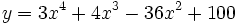- c)
.
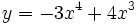Solución:
Utiliza la siguiente escena para comprobar los resultados.
Representación gráfica de funciones Descripción: En la siguiente escena puedes ver la representación gráfica de distintas funciones.
