Vectores: Producto escalar (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Act. Interactivas | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Producto escalar de vectores
Se llama producto escalar de dos vectores 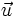 y
y 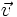 , al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
, al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
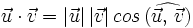
Propiedades del producto escalar
Propiedad fundamental del producto escalar
Propiedades (1)
- Si
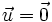 ó
ó 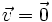 entonces
entonces 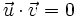 .
.
-
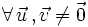 se cumple que
se cumple que 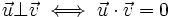
- La primera propiedad es inmediata.
- Para la segunda propiedad, si ambos vectores no son nulos, entonces, para que el producto escalar sea cero, debe ser cero el coseno del ángulo que forman, y esto ocurre sólo si el ángulo es de 90º.
Signo del producto escalar
Propiedades (2)
El signo del producto escalar queda determinado por el ángulo que forman los vectores:
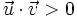 si
si 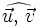 es agudo.
es agudo.
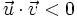 si
si 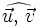 es obtuso.
es obtuso.
Esta propiedad es inmediata, ya que el coseno de un ángulo es positivo, si éste es agudo, y negativo, si es obtuso.
En esta escena podrás ver como se calcula el producto escalar de vectores y cómo es su signo.
Operaciones con el producto escalar
Propiedades (3)
- Conmutativa:
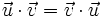 .
.
- Asociativa mixta:
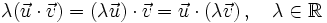 .
.
- Distributiva:
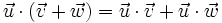 .
.
- Propiedad conmutativa:
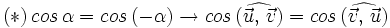
- Propiedad asociativa:
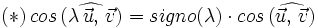 , ya que el ángulo es igual si
, ya que el ángulo es igual si 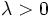 y suplementario si
y suplementario si 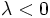 .
.
- (Recuerda que ángulos suplementarios tienen cosenos opuestos).
- Así tenemos una de las igualdades:
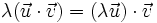 . La otra igualdad se obtendría de forma similar.
. La otra igualdad se obtendría de forma similar.
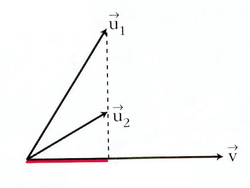
- Propiedad distributiva:
- Obteniendo la igualdad buscada.
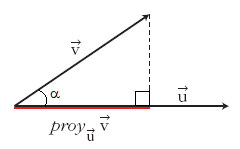
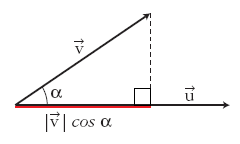
Proyección de vectores y producto escalar
Llamaremos proyección del vector 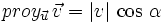 siendo Observa que la proyección es un número positivo o negativo según lo sea |
Corolario (5): Proyecciones coincidentes Si las proyecciones sobre 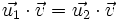 Demostración:  En esta escena podrás ver como se representa y calcula la proyección de un vector sobre otro. |
Ejercicios propuestos
|
Ejercicios propuestos: Producto escalar |
El producto escalar con bases ortonormales
Expresión analítica del producto escalar en bases ortonormales
Proposición (6)
Sea 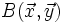 una base ortonormal, entonces
una base ortonormal, entonces
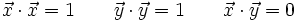
En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos:
Proposición (7)
Si las coordenadas de los vectores 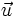 y
y 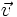 , respecto de una base otonormal
, respecto de una base otonormal 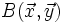 son
son 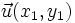 y
y 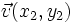 , entonces:
, entonces:
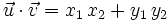
En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos:
En esta escena podrás ver como se representa el producto escalar de dos vectores.
Vector ortogonal a otro
Proposición (10)
Los vectores de coordenadas 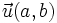 y
y 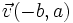 , respecto de una base ortonormal, son ortogonales.
, respecto de una base ortonormal, son ortogonales.
Por la propiedad fundamental, sabemos que:
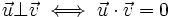
Por otro lado, como las base es ortonormal, la expresión analítica del producto escalar es

Halla 3 vectores ortogonales a (2,3).
Solución: Por la proposición anterior: (-3,2).
Cualquier múltiplo de (-3,2) también será ortogonal: (3,-2) y (-6,4)
Ejemplo:
Calcula el valor de 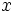 para que el vector
para que el vector 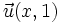 sea ortogonal a
sea ortogonal a 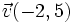 , respecto de una base ortonormal.
, respecto de una base ortonormal.
Al venir dadas las coordenadas respecto de una base ortonormal, para que los vectores dados sean ortogonales, su producto escalar debe ser cero:
En esta escena podrás ver como es el producto escalar de vectores ortogonales.
Módulo de un vector en una base ortonormal
Proposición (8)
El módulo de un vector 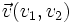 , respecto de una base otonormal, es
, respecto de una base otonormal, es
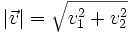
Si 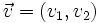 respecto de una base otonormal, entonces:
respecto de una base otonormal, entonces:
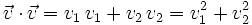
Por otro lado:
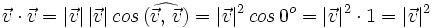
- Módulo de un vector.
- Ejemplos.
Nota: En la segunda parte del video se trata el caso de vectores tridimensionales.
- Vector unitario.
- Ejemplos de como calcularlos.
Nota: En la segunda parte del video se trata el caso de vectores tridimensionales.
- Módulo de un vector.
- Ejemplos.
- Vectores unitarios.
Dados los vectores 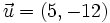 y
y 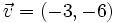 , calcula:
, calcula:
- a)
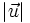
- b)
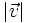
- c)
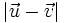
Ángulo de dos vectores en una base ortonormal
Proposición (9)
Dados dos vectores, 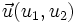 y
y 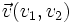 , respecto de una base otonormal, se cumple que
, respecto de una base otonormal, se cumple que
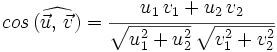
Si 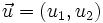 y
y 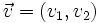 , respecto de una base otonormal, entonces:
, respecto de una base otonormal, entonces:
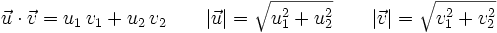
Por otro lado:
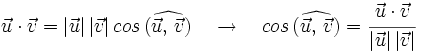
Dados los vectores 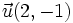 y
y 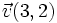 , respecto de una base otonormal, vamos a calcular el ángulo que forman:
, respecto de una base otonormal, vamos a calcular el ángulo que forman:
Ejercicios propuestos
|
Ejercicios propuestos: Producto escalar con bases ortonormales |
Producto escalar de vectores (enfoque alternativo)
En estos videotutoriales se va partir de la proposición (7) como definición de producto escalar y se va a deducir como resultado la definición de la que hemos partido al comienzo de este capítulo.
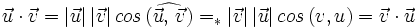
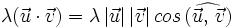
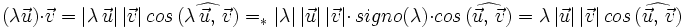

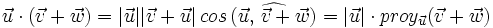
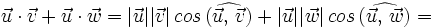
![=|\vec{u}|[|\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})+|\vec{w}| \, cos \, (\widehat{\vec{u}, \, \vec{w}})]=](/wikipedia/images/math/f/3/b/f3b89089f996e680f6647e40232d1b7a.png)
![=|\vec{u}| \cdot [proy_\vec{u} \vec{v}+proy_\vec{u} \vec{w}]=|\vec{u}| \cdot [proy_\vec{u} (\vec{v}+ \vec{w})]](/wikipedia/images/math/a/4/6/a466b34f8c309d0f85cdbd073cd479e5.png)
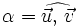
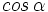 .
.
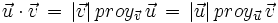
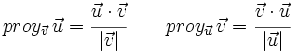
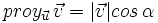
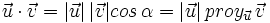
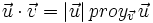
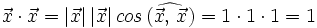
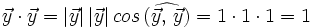
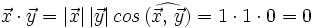
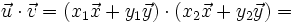
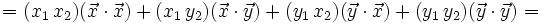
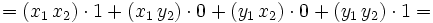
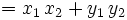
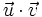
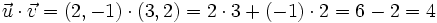
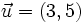 y
y 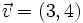 . Halla el producto escalar
. Halla el producto escalar  para que los vectores
para que los vectores 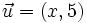 y
y 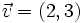 sean ortogonales.
sean ortogonales.
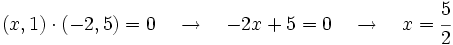
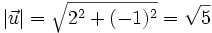
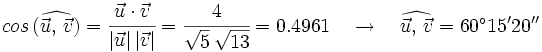
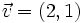 .
.
