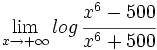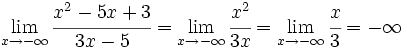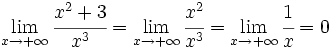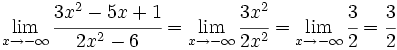Plantilla:Límite de funciones racionales cuando x tiende a infinito
De Wikipedia
Proposición
Consideremos la función racional en la variable x, ya simplificada:
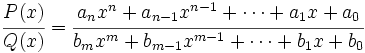
Se cumple que:
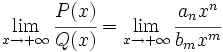 (análogamente si
(análogamente si 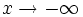 )
)Se pueden dar los siguientes casos:
- grado(P) > grado(Q): tras simplificar la fracción queda el límite de una función polinómica, que ya sabemos calcular, y que sabemos que puede ser
 ó
ó  .
.
- grado(P ) = grado(Q): tras simplificar la fracción queda una constante,
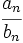 , que es el valor del límite.
, que es el valor del límite.
- grado(P) < grado(Q): tras simplificar la fracción queda una función inversa de una polinómica, cuyo límite sabemos que vale 0.
Para calcular el límite de un cociente de polinomios cuando x → +∞ o cuando x → -∞, dividimos numerador y denominador por la mayor potencia de "x" que aparezca en el denominador.
- Si numerador y denominador son de igual grado, el límite es el cociente de los coeficientes de los términos de mayor grado del numerador y el denominador.
- Si el numerador es de menor grado que el denominador, el límite es 0.
- Si el numerador es de mayor grado que el denominador, el límite es +∞ ó -∞ según que el numerador y el denominador tengan igual signo o no.
Calcula: 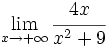
Calcula: 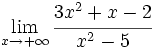
Calcula: