Límite de una función (2ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Límite de de una función en un punto
El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto.
De manera informal, diremos que una función 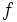 tiene límite
tiene límite 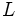 en
en 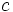 , o que
, o que 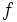 tiende a
tiende a 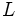 cuando x se acerca a
cuando x se acerca a 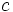 si se puede hacer que
si se puede hacer que 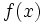 esté tan cerca como queramos de
esté tan cerca como queramos de 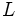 haciendo que
haciendo que 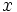 esté suficientemente cerca de
esté suficientemente cerca de 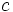 , siendo
, siendo 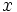 distinto de
distinto de 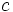 .
.
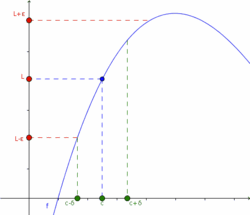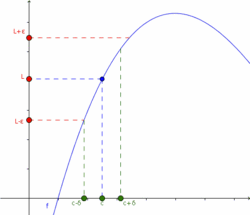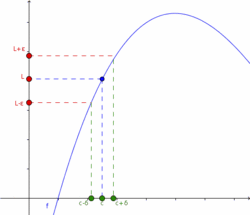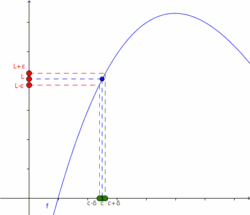
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función  , cuando
, cuando 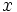 tiende a
tiende a 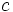 , es
, es 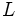 , si y sólo si, para todo
, si y sólo si, para todo 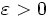 , existe un
, existe un 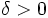 , tal que para todo número real
, tal que para todo número real 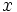 en el dominio de la función, si
en el dominio de la función, si 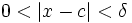 entonces
entonces 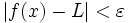 .
.
Esto, escrito en notación formal:
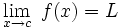
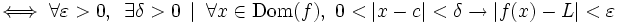
Esta es una formulación estricta del concepto de límite de una función real en un punto de acumulación del dominio de la función y se debe al matemático francés Luis Cauchy.