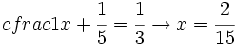Plantilla:Resolución de problemas mediante ecuaciones de primer grado
De Wikipedia
Procedimiento
Para resolver un problema mediante una ecuación hay que seguir los siguientes pasos:
- Determinar la incógnita.
- Traducir el enunciado del problema al lenguaje algebraico mediante una ecuación en la que intervenga la incógnita.
- Resolver la ecuación, es decir, hallar el valor de la incógnita.
- Dar la solución del problema a partir del valor obtenido de la incógnita.
Aquí tienes una colección de problemas con un nivel de dificultad bajo para que vayas cogiendo práctica.
Pulsa el botón EJEMPLO para ver más problemas.
Pulsa el botón DATOS para ver otro problema similar, pero con datos diferentes.
Actividades en la que aprenderás a resolver problemas con ecuaciones de primer grado de distintos tipos.
Como se traducen expresiones del lenguaje cotidiano a expresiones algebraicas y su uso en el planteamiento de ecuaciones.
2 problemas.
1 problema.
2 problemas.
1 problema.
2 problemas.
1 problema.
1 problema.
Al levantarse por la mañana, el ratoncito Pérez encuentra un trozo de pan. Se come 3/5 para desayunar y 7/8 del resto para merendar, con lo que le quedan 10 gramos para la cena. ¿Cuanto pesaba el pan?
- Determina el respectivo precio de bocadillos y refrescos en un bar si un bocadillo cuesta un euro más que un refresco y el importe de una consumición de 3 refrescos y 5 bocadillos es de 2 euros.
- Tres hermanos tienen respectivamente 7,9 y 12 años, y su madre 36 años. ¿Cuántos años deben pasar para que la edad de la madre sea suma de las edades de sus hijos?
- La edad de un hijo es la quinta parte de la de su padre, y dentro de 7 años, la edad del padre triplicara la del hijo. ¿Qué edad tiene cada uno?
- Un hijo tiene 30 años menos que su padre, y la edad de este cuadruplica la de aquél. ¿Qué edad tiene cada uno?
Un reloj marca las 6 en punto. ¿A qué hora forman las agujas por primera vez un ángulo de 92 grados?
Un reloj marca las 6 en punto. ¿A qué hora forman las agujas por segunda vez un ángulo de 90 grados?
Un reloj marca las 6 en punto. ¿A qué se superponen las agujas por primera vez?
Los ángulos de un triángulo miden 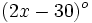 ,
, 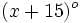 y
y 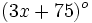 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Los ángulos de un cuadrilátero miden 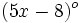 ,
, 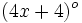 ,
, 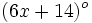 y
y 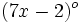 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
3 problemas con números consecutivos
Determinar el área de un rectángulo que tiene 60 cm de perímetro, si la razón entre sus lados es 3:2.
Hallar tres números consecutivos cuya suma sea igual al doble del mayor, incrementado en 26.
Un comerciante tiene 3000$ para invertir en dos negocios: uno que produce un 5% de beneficio y otro un 9%. ¿Qué cantidad debe destinar a cada negocio para conseguir un rendimiento neto del 8% con ese capital?.
Si tenemos 2000$ para invertir al 6% y al 8.5% anual, ¿cuánto deberemos destinar a cada inversión con el fin de obtener un rendimiento total de 300$ después de 2 años?.
Una empresa fabrica un artículo con un coste variable por unidad de 3$. Si los costes fijos son de 75000$ y cada artículo se vende por 5$, ¿cuántas unidades deben producirse y vender para que la empresa obtenga unos beneficios de 40000$?
Vídeotutorial con 4 problemas que se resuelven utilizando ecuaciones.
Tutorial practico en el que aparecen dos problemas resueltos mediante ecuaciones. Estos problemas son del tipo en el que se reparte algo entre varias personas y existe una relación entre lo que recibe cada uno de ellos.
Problema con porcentajes.
2 problemas.
1 problema.
1 problema.
1 problema.
1 problema.
1 problema.
1 problema.
Problema de mezclas con sales de baño.
Se dispone de dos clase de café: uno de 1.05$ y otro de 1.25$ la libra. ¿Qué cantidad se utiliza de cada uno para obtener café de 1.20$ la libra, si de la clase más cara se utilizan 20 libras más que de la barata?
¿Cuántos litros de una solución de alcohol al 30% deben mezclarse con 90 litros de otra solución al 70% para obtener una solución al 60%?
Si tienes 50 onzas de una solución salina al 25% (mezcla de agua con sal), ¿Cuántas onzas de solución salina al 10% debes agregar para obtener una nueva solución salina al 15%?
Un biólogo realiza una investigación sobre el impacto de tres diferentes bebidas azucaradas a base de agua en la habilidad de las abejas de producir miel. Coge 2 litros de la bebida A, que contiene 40% de azúcar, y agrega 1.2 litros de bebida B. Comprobó que las abejas preferían esta nueva solución, que llamaremos bebida C, la cual medimos que contiene 25% de azúcar. ¿Cuál es el porcentaje de azúcar de la bebida B?
Problema en el que la incógnita es la medida de la longitud de un segmento de recta.
Problema en el que la incógnita es la medida de la longitud de un segmento de recta.
Problema en el que la incógnita es la medida de la longitud de un segmento de recta.
Problema en el que la incógnita es la medida de la longitud de un segmento de recta.
Problema en el que la incógnita es la medida de la longitud de un segmento de recta.
Problema en el que la incógnita es la medida de la longitud de un segmento de recta.
Ejercicios resueltos
- Un repostero ha mezclado 12 kg de azúcar de 1.10 €/kg con una cierta cantidad de miel de 4.20 €/kg para que la mezcla le salga a 2.34 €/kg. ¿Cuánta miel tuvo que poner?
- La distancia entre dos ciudades, A y B, es de 280 km. Untren sale de A hacia B a 80 km/h, y media hora más tarde sale un coche de B hacia A que tarda 1.2 horas en cruzarse con el tren. ¿Qué velocidad lleva el coche?
- Tres amigos trabajan 20, 30 y 50 días en un negocio. Al cabo de tres meses se reparten los beneficios y al tercero le corresponden 300 € más que al segundo. ¿Cuál es la cantidad repartida?
- Dos grifos llenan un depósito en 3 horas. Si sólo se abre uno de ellos, tardaría 5 horas. ¿Cuánto tardará el otro grifo en llenar el depósito?
Solución 1:
x = kg de miel
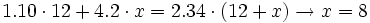 kg de miel
kg de miel
Solución 2:
x = velocidad del coche
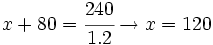 km/h
km/h
Solución 3:
x = beneficio del 1º
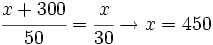 € corresponden al primero.
€ corresponden al primero.
y = beneficio del 2º
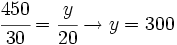 € corresponden al segundo.
€ corresponden al segundo.
La cantidad repartida es : 300+450+750=1500 €
Solución 4:
1/5 = fracción de depósito que llena uno de los grifos en 1 h
x = fracción de depósito que llena el otro grifo en 1 h
Problemas de autoevaluación sobre móviles.
Problemas de autoevaluación sobre relojes.
Problemas de autoevaluación sobre grifos.
Problemas de autoevaluación de mezclas.
Problemas de autoevaluación de aleaciones.
Problemas de autoevaluación geométricos.
Problemas resueltos con ecuaciones de primer grado.
Problemas resueltos con ecuaciones de primer grado.