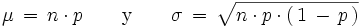Distribuciones continuas: La distribución normal

De Wikipedia

Revisión de fecha 14:14 1 jul 2007; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Saltar a navegación, búsqueda

Tabla de contenidos

1 Función de densidad
- 1.1 Definición
- 1.2 Ejemplo
2 Función de distribución
- 2.1 Definición
- 2.2 Ejemplo
3 Distribución normal
- 3.1 Definición
- 3.2 Ejemplo

Función de densidad

Definición

Una función 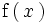$\mathrm{f}\left( \, x \, \right)$ es la función de densidad de una variable continua $X$ si cumple:

1. 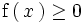$\mathrm{f} \left( \, x \, \right) \ge 0$ en todo $x$ del intervalo en el que está definida.

2. El área total entre la curva y el eje de abscisas es uno.

3. La probabilidad de que la variable tome valores del intervalo $\left[ \, x_i, \, x_j \, \right]$ es el área bajo el trozo de curva correspondiente a dicho intervalo.

Ejemplo

La función de densidad de una variable aleatoria continua $X$ , cuyos valores se distribuyen uniformemente en $\left[ \, a, \, b \, \right]$ , se define de la siguiente manera:

No se pudo entender (función desconocida\begin): \mathrm{f} \left( \, x \, \right) \, = \, \left\{ \begin{array}[c]{ccc} \frac{1}{b \, - \, a} & \mathrm{si} & x \in \left[ \, a, \, b \, \right] \\ 0 & \mathrm{si} & x \not\in \left[ \, a, \, b \, \right] \end{array} \right.

Función de distribución

Definición

Una función 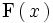$\mathrm{F}\left( \, x \, \right)$ es la función de distribución de una variable aleatoria $X$ si:

1. La derivada de 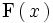$\mathrm{F}\left( \, x \, \right)$ es la función de densidad de la variable $X$ .

2. 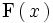$\mathrm{F}\left( \, x \, \right)$ es cero para todos los valores menores que el menor valor de la variable.

3. 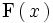$\mathrm{F}\left( \, x \, \right)$ es uno para todos los valores mayores que el mayor valor de la variable.

Ejemplo

La función de distribución de una variable aleatoria continua $X$ , cuyos valores se distribuyen uniformemente en $\left[ \, a, \, b \, \right]$ , se define de la siguiente manera:

No se pudo entender (función desconocida\begin): \mathrm{F}\left( \, x \, \right) \, = \, \left\{ \begin{array}[c]{ccc} 0 & \mathrm{si} & a > x \\ \frac{x \, - \, a}{b \, - \, a} & \mathrm{si} & x \in \left[ \, a, \, b \, \right] \\ 1 & \mathrm{si} & x > b \end{array} \right.

Distribución normal

Definición

Una variable aleatoria continua $X$ sigue una distribución normal de media $μ$ y desviación tipica $σ$ , si verifica las siguientes condiciones:

1. El recorrido de la variable $X$ es toda la recta real.

2. La función de densidad es de la siguiente forma:

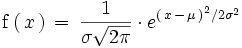
$\mathrm{f} \left( \, x \, \right) \, = \, \frac{1}{\sigma \sqrt{2 \pi}} \cdot e^ { \left( \, x \, - \, \mu \, \right) ^ 2 / 2\sigma^2 }$

La distribución normal describe fenómenos en cuyo resultado final interviene gran número de factores independientes entre sí. Las principales características de la función de densidad de la distribución normal son las siguientes:

1. Es simétrica respecto de la recta 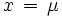$x \, = \, \mu$ , pues:

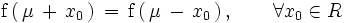
$\mathrm{f} \left( \, \mu \, + \, x_0 \, \right) \, = \, \mathrm{f} \left( \, \mu \, - \, x_0 \, \right) , \qquad \forall x_0 \in R$

2. Posee un máximo en el punto de abscisa 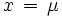$x \, = \, \mu$ , y no tiene mínimos.

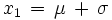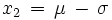3. Tiene dos puntos de inflexión en los puntos de abscisa $x_1 \, = \, \mu \, + \, \sigma$ y $x_2 \, = \, \mu \, - \, \sigma$ .

4. El eje de abscisas es una asíntota de la curva.

Si la variable aleatoria $X$ sigue una distribución normal de parámetros $μ$ y $σ$ , entonces:

1. La probabilidad de que 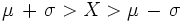$\mu \, + \, \sigma > X > \mu \, - \, \sigma$ es 0,6825.

2. La probabilidad de que 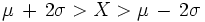$\mu \, + \, 2 \sigma > X > \mu \, - \, 2 \sigma$ es 0,9544.

3. La probabilidad de que 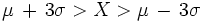$\mu \, + \, 3 \sigma > X > \mu \, - \, 3 \sigma$ es 0,9973.

La distribución binomial se puede aproximar por la normal si se cumple que:

$n \cdot p \ge 5 \qquad \mathrm{y} \qquad n \cdot \left( \, 1 \, - \, p \, \right) \ge 5$

Ejemplo

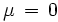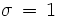La distribución normal estándar es la distribución normal con $\mu \, = \, 0$ y $\sigma \, = \, 1$ .

Cuando estas condiciones se verifican la distribución normal se aproxima a la distribución normal de parametros:

$\mu \, = \, n \cdot p \qquad \mathrm{y} \qquad \sigma \, = \, \sqrt { n \cdot p \cdot \left( \, 1 \, - \, p \, \right) }$

Obtenido de "http://maralboran.org/wikipedia/index.php/Distribuciones_continuas:_La_distribuci%C3%B3n_normal"

Distribuciones continuas: La distribución normal

De Wikipedia

Tabla de contenidos

Función de densidad

Definición

Ejemplo

Función de distribución

Definición

Ejemplo

Distribución normal

Definición

Ejemplo

Vistas

Herramientas personales

Menú

Buscar

Herramientas