Plantilla:Representación gráfica de una función
De Wikipedia
La representación gráfica de una función nos permite visualizar el comportamiento de las dos variables.
Procedimiento
- Usaremos un sistema de ejes cartesianos con una escala adecuada.
- Sobre el eje horizontal (eje de abscisas) representamos la variable independiente
 .
.
- Sobre el eje vertical (eje de ordenadas) la variable dependiente
 .
.
- Sobre el eje horizontal (eje de abscisas) representamos la variable independiente
- Cada punto de la gráfica es generado por una pareja de valores
 e
e  , que son sus coordenadas
, que son sus coordenadas 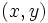 , su abscisa y su ordenada.
, su abscisa y su ordenada.
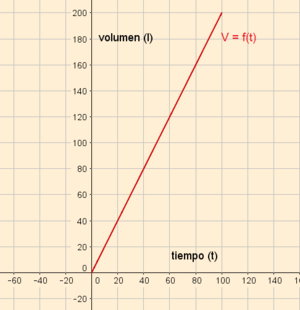
Consideremos el ejemplo anterior del grifo y el depósito:
- "Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
Función:
El volumen del depósito es función del tiempo: 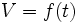
- t = "Tiempo que está abierto el grifo" (en segundos).
- V = "Volumen de agua que se ha llenado el depósito" (en litros).
Tabla de valores:
Para obtener la representación gráfica es necesario obtener puntos de la misma. Para ello construiremos la llamada tabla de valores, que consiste en averiguar parejas de valores (t,V) que estén relacionadas mediante la función:
tiempo (s) |
0 | 1 | 5 | 20 | 40 | 60 | 100 |
Volumen (l) |
0 | 2 | 10 | 40 | 80 | 120 | 200 |
Gráfica:
- Representaremos los valores de la tabla en unos ejes de coordenadas. Cada punto de la gráfica consta de dos coordenadas: la primera es el valor de t y la segunda, el valor de V.
Representación de puntos en el plano cartesiano.
Cómo encontrar los puntos en el plano cartesiano.
Conocemos el plano cartesiano, como ubicar un punto por medio de una pareja de coordenadas. Las partes del plano, que son las abscisas, las ordenadas, el eje X, el eje Y y otros conceptos.
Representación de puntos en el plano cartesiano.
El Sistema de Referencia Cartesiano Plano permite identificar enequívocamente los puntos del plano mediante el eje de abcisas (x), y el eje de odenadas (y).
En esta clase veremos qué son las coordenadas de un punto y cómo se representa un punto cualquiera en el plano a partir de sus coordenadas.
Qué es la geometría analítica. Ejes de coordenadas y puntos.
Video-presentación sobre el plano cartesiano. Al final tienes dos ejercicios propuestos con sus soluciones.
Dibuja unos ejes cartesianos y ubica los puntos (2,4), (-2,3), (5,-4), (-6,4) y (0,3).
Dibuja unos ejes cartesianos y ubica los puntos (-3,4), (2,3), (-1,-3), (2,-4) y (0,0).
1) Escribe las coordenadas de los puntos representados gráficamente.
2) Dibuja los puntos A(-2,2), B(5,6), C(-1,0), D(-2,-3), E(0,5), F(-4,7) en unos ejes cartesianos.
3) Dibuja los puntos A(1,3), A'(-1,3), B(2,5), B'(-2,5), C(4,7), C'(-4,7) en unos ejes cartesianos.
4) Dibuja los puntos A(2,2), B(2,-2), C(-2,2), D(-2,-2) en unos ejes cartesianos.
5) Representa cinco puntos con la misma ordenada en unos ejes cartesianos.
6) Representa cinco puntos con la misma abscisa en unos ejes cartesianos.
7) Representa cinco puntos con la misma abscisa y ordenada en unos ejes cartesianos.
Representa el punto (6,-8) en el plano coordenado.
Indica cuál de los puntos dados mediante sus coordenadas no está representado en lo ejes coordenados.
¿En qué cuadrante se encuentra ubicado el punto (-7,7)?
Representa cada uno de los siguientes puntos e indica en qué cuadrante se encuentran ubicados:
- a) (-2.5,2) b) (-5,-9) c) (2, -6)
- Representa los puntos (2,4) y (2, -8) en el plano coordenado y averigua la distancia que hay entre ellos.
- Interpretación de una gráfica dada.
- Representa los puntos (-8,7) y (5, 7) en el plano coordenado y averigua la distancia que hay entre ellos.
Ejercicios sobre puntos reflejados.
- Indica las coordenadas de los puntos representados en el plano cartesiano.
- Dibuja los puntos A(4,2), B(-3,5.5), C(4,-4) y D(-2,-3) en unos ejes cartesianos.
- Los puntos A(-4,-4), B(3,-4) y C(3,3) son tres de los vértices del cuadrado ABCD. Dibújalos en el plano cartesiano y determina las coordenadas del punto D.
Actividades en las que podrás aprender a:
- Identificar los elementos de la representación cartesiana: ejes, origen, ordenda, abscisa, puntos, coordenadas...
- Representar puntos con coordenadas enteras.
- Representar puntos con coordenadas decimales.
- Distinguir el cuadrante en que se encuentra un punto, conocidas sus coordenadas.
Actividad en la que aprenderás a representar gráficamente una función a partir de su tabla de valores. Las funciones son las que sirvieron de ejemplo en la actividad del apartado anterior.
En esta escena podrás ver como se representan los puntos de la gráfica de una función en unos ejes de coordenadas cartesianos.
Interpretación de gráficas
{´Videotutoriales|titulo=Interpretación de gráficas|enunciado=
La primera parte del tutorial recuerda los conceptos básicos sobre funciones: variable independiente, dependiente, imagen, preimagen, dominio, recorrido... En la segunda parte se muestran ejemplos de funciones dadas mediante gráficas.
Ejemplo de cómo se pueden usar las gráficas de forma engañosa en publicidad.
}}
Función que relaciona el tiempo que lleva abierto un grifo y la altura que alcanza el nivel del agua en un depósito cilíndrico.
La siguiente escena representa una botella (en color rojo) que cuando abras el grifo se comenzará a llenar de agua. El proceso de llenado de la botella se puede describir matemáticamente con lo que llamamos función, así para un tiempo concreto la función nos dice la altura de la botella en ese momento. El dibujo que queda tras el punto A se llama gráfica de la función.
Haz clic en el botón y dejándolo pulsado observa cómo se llena la botella .
Observa que en el eje horizontal representamos el tiempo que dejamos el grifo abierto y en el vertical la altura que el agua alcanza en la botella. En el eje horizontal hemos empezado a marcar 1 segundo, 2 segundos, etc.
Observa en este ejemplo, que la altura es cero cuando el tiempo transcurrido es cero y que la gráfica va creciendo.
- a) Observa las alturas que se alcanzan cuando han transcurrido 2, 4 y 6 segundos. Anótalas.
Si haces clic sobre un punto con el cursor te aparecerán los valores horizontal (tiempo) y vertical (altura) para ese punto.
- b) ¿Qué puedes decir de la relación entre las variables tiempo y altura?
- c) ¿Cuánto tiempo necesita la botella para llenarse hasta la mitad?
- d) ¿Cuánto tiempo necesita la botella para llenarse un cuarto? ¿Y tres cuartos?
Función que relaciona el tiempo que lleva abierto un grifo y la altura que alcanza el nivel del agua en un depósito de forma cónica.
En la siguiente escena la forma de la botella ha cambiado.
- a) Intenta hacer la gráfica antes de ver como queda en la escena.
- b) Observa las alturas que se alcanzan cuando han transcurrido 2, 4 y 6 segundos. Anótalas.
- c) ¿Qué puedes decir de la relación entre las alturas y los tiempos?
- d) Ahora la altura del agua según pasa el tiempo sube más despacio, ¿por qué?
Ahora prueba a cambiar la forma de la botella moviendo el punto P.
- e) Haz una botella con la boca más estrecha que la base y observa las distintas gráficas que se generan. Da una explicación de lo qué ocurre.
- f) Las gráficas unas veces son convexas (tipo U) y otras cóncavas (tipo U invertida), ¿de qué depende?
Evalúa funciones a partir de su gráfica.
Evalúa expresiones con funciones.