Ecuaciones de primer grado con dos incógnitas (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 160)
Ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas o ecuación lineal con dos incógnitas es una ecuación polinómica de primer grado con dos incógnitas. Por tanto, se puede expresar de la siguiente forma general:
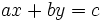
donde  e
e  son variables (incógnitas) y
son variables (incógnitas) y 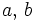 y
y  constantes (números reales).
constantes (números reales).
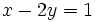 (es de primer grado con 2 incógnitas)
(es de primer grado con 2 incógnitas)
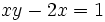 (no es de primer grado, aunque si tiene dos incógnitas)
(no es de primer grado, aunque si tiene dos incógnitas)
Soluciones de una ecuación de primer grado con dos incógnitas
Las soluciones de una ecuación lineal con dos incógnitas 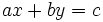 son las parejas de valores
son las parejas de valores 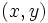 que hacen que se cumpla la igualdad.
que hacen que se cumpla la igualdad.
Proposición
Una ecuación de primer grado con dos incógnitas 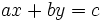 tiene infinitas soluciones.
tiene infinitas soluciones.
Para cada valor que le asignemos a la variable  , podemos encontrar un valor de la variable
, podemos encontrar un valor de la variable  , despejándola en la anterior ecuación, como se muestra a continuación:
, despejándola en la anterior ecuación, como se muestra a continuación:
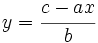
La ecuación 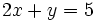 tiene infinitas soluciones que se pueden obtener dando valores a la variable
tiene infinitas soluciones que se pueden obtener dando valores a la variable  y despejando la variable
y despejando la variable  :
:
- Si
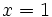 , entonces
, entonces 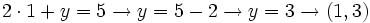
- Si
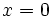 , entonces
, entonces 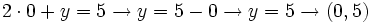
También podemos hallar el valor de  a partir de cualquier valor de
a partir de cualquier valor de  dado. En este caso habrá´que despejar la
dado. En este caso habrá´que despejar la  :
:
- Si
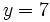 , entonces
, entonces 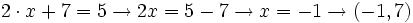
...
Dada la ecuación -3x - y = 6, indica cuáles de los siguientes pares son solución de ella: (-4,4) y (-3,3).
Dada la ecuación 4x - 1 = 3y + 5, indica cuáles de los siguientes pares son solución de ella: (3,2) y (2,3).
Soluciones de ecuaciones lineales de dos variables.
Completa soluciones de ecuaciones lineales de dos variables.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones de primer grado con dos incógnitas |
(Pág. 161)
Representación gráfica de las soluciones de una ecuación lineal con dos incógnitas
Proposición
Las parejas de soluciones 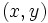 de una ecuación lineal con dos incógnitas, representadas como puntos en un sistema de ejes cartesianos, forman una recta.
de una ecuación lineal con dos incógnitas, representadas como puntos en un sistema de ejes cartesianos, forman una recta.
- El punto de corte con el eje de abscisas (OX), que se obtiene para
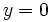 , recibe el nombre de abscisa en el origen.
, recibe el nombre de abscisa en el origen.
- El punto de corte con el eje de ordenadas (OY), que se obtiene para
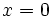 , recibe el nombre de ordenada en el origen.
, recibe el nombre de ordenada en el origen.
Ejemplo: Representación gráfica de las soluciones de una ecuación lineal con dos incógnitas
Halla y representa las soluciones de la ecuación:
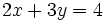
Despejamos la variable y:
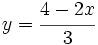
Construimos una tabla de valores, dandole valores a  y calculando
y calculando  en la expresión anterior:
en la expresión anterior:
| x | -1 | 2 | 5 | ... |
| y | 2 | 0 | -2 | ... |
Las soluciones vienen dadas por las parejas 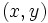 así obtenidas:
así obtenidas:
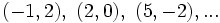
Si representamos estas soluciones como puntos de unos ejes de coordenadas, comprobaremos que se encuentran situados en una línea recta, como puedes ver en la siguiente escena.
Comprueba que los puntos solución se encuentran en la recta azul. Para ello deberás introducir el valor de  en el cuadro inferior y pulsar "Intro":
en el cuadro inferior y pulsar "Intro":
Calcula algunas soluciones más y compruébalas en la escena anterior.
Concluyendo: Las soluciones de una ecuación de primer grado con dos incógnitas son infinitas y los puntos que se obtienen con sus coordenadas, están situados en una recta.Representación de puntos en el plano cartesiano.
Cómo encontrar los puntos en el plano cartesiano.
Conocemos el plano cartesiano, como ubicar un punto por medio de una pareja de coordenadas. Las partes del plano, que son las abscisas, las ordenadas, el eje X, el eje Y y otros conceptos.
Representación de puntos en el plano cartesiano.
El Sistema de Referencia Cartesiano Plano permite identificar enequívocamente los puntos del plano mediante el eje de abcisas (x), y el eje de odenadas (y).
En esta clase veremos qué son las coordenadas de un punto y cómo se representa un punto cualquiera en el plano a partir de sus coordenadas.
Qué es la geometría analítica. Ejes de coordenadas y puntos.
Video-presentación sobre el plano cartesiano. Al final tienes dos ejercicios propuestos con sus soluciones.
Dibuja unos ejes cartesianos y ubica los puntos (2,4), (-2,3), (5,-4), (-6,4) y (0,3).
Dibuja unos ejes cartesianos y ubica los puntos (-3,4), (2,3), (-1,-3), (2,-4) y (0,0).
1) Escribe las coordenadas de los puntos representados gráficamente.
2) Dibuja los puntos A(-2,2), B(5,6), C(-1,0), D(-2,-3), E(0,5), F(-4,7) en unos ejes cartesianos.
3) Dibuja los puntos A(1,3), A'(-1,3), B(2,5), B'(-2,5), C(4,7), C'(-4,7) en unos ejes cartesianos.
4) Dibuja los puntos A(2,2), B(2,-2), C(-2,2), D(-2,-2) en unos ejes cartesianos.
5) Representa cinco puntos con la misma ordenada en unos ejes cartesianos.
6) Representa cinco puntos con la misma abscisa en unos ejes cartesianos.
7) Representa cinco puntos con la misma abscisa y ordenada en unos ejes cartesianos.
Representa el punto (6,-8) en el plano coordenado.
Indica cuál de los puntos dados mediante sus coordenadas no está representado en lo ejes coordenados.
¿En qué cuadrante se encuentra ubicado el punto (-7,7)?
Representa cada uno de los siguientes puntos e indica en qué cuadrante se encuentran ubicados:
- a) (-2.5,2) b) (-5,-9) c) (2, -6)
- Representa los puntos (2,4) y (2, -8) en el plano coordenado y averigua la distancia que hay entre ellos.
- Interpretación de una gráfica dada.
- Representa los puntos (-8,7) y (5, 7) en el plano coordenado y averigua la distancia que hay entre ellos.
Ejercicios sobre puntos reflejados.
- Indica las coordenadas de los puntos representados en el plano cartesiano.
- Dibuja los puntos A(4,2), B(-3,5.5), C(4,-4) y D(-2,-3) en unos ejes cartesianos.
- Los puntos A(-4,-4), B(3,-4) y C(3,3) son tres de los vértices del cuadrado ABCD. Dibújalos en el plano cartesiano y determina las coordenadas del punto D.
Descartes: Un puente entre el álgebra y la geometría.
Ecuación lineal. Representación gráfica.
Una ecuación (lineal o no) con dos incógnitas tiene infinitas soluciones. En términos geométricos, si la ecuación es lineal, las infinitas soluciones corresponden a los infinitos puntos de una recta.
Dada la ecuación 2x + 3y = 5x - y, completa la tabla que aparee en el video y utiliza los resultados para representar gráficamente las soluciones.
Representa las soluciones de la ecuación lineal y = 2x - 3.
Representa las soluciones de 2x + 3y = 6.
Halla, en cada caso, el valor de "k" de modo que el par ordenado sea solución de 2x-y=3.
1. 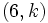 2.
2. 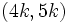 3.
3. 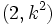 4.
4. 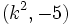 5.
5. 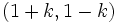
Representa y halla los puntos de corte con los ejes de las gráficas de las ecuaciones:
- a)
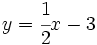
- b)
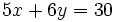
Halla la intersección con el eje X de la gráfica de la ecuación 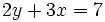
Halla las intersecciones con los ejes de la gráfica de la ecuación 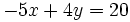 y utiliza la información para representar la gráfica de la ecuación.
y utiliza la información para representar la gráfica de la ecuación.
Halla la intersección con el eje Y de la gráfica de la ecuación lineal dada por una tabla (ver video).
Actividades en la que aprenderás a obtener las soluciones de una ecuación lineal con dos incógnitas y a representarlas gráficamente.
Escena en la que podrás calcular y representar las soluciones de una ecuación lineal con dos incógnitas.
Escena en la que podrás comprobar si sabes calcular las soluciones de una ecuación lineal con dos incógnitas.
Intersecciones a partir de una gráfica.
Intersecciones a partir de una ecuación.
Intersecciones a partir de una tabla.
|
Actividad: Ecuación lineal con dos incógnitas Considera la ecuación
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios propuestos
|
Ejercicios propuestos: Representación gráfica de las soluciones de una ecuación lineal con dos incógnitas |
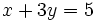 porque si
porque si  e
e 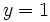 , entonces
, entonces 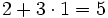 .
.
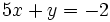 :
:

