Plantilla:La pendiente y el crecimiento en la función afín
De Wikipedia
Propiedades
La pendiente, 
, describe el crecimiento de la función 
:
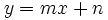- Si
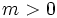, la función es creciente.
- Si
la función es decreciente.
- Si
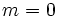la función es constante (recta horizontal).
Además, cuanto mayor es su pendiente (en valor absoluto), más inclinada es su gráfica.
{{Videotutoriales|titulo=La pendiente y el crecimiento|enunciado=
Tutorial (4'44") Sinopsis: Pendiente de una recta. Significado del signo de la pendiente.
La pendiente y el crecimiento Descripción: En esta escena podrás ver como afecta el signo de la pendiente al crecimiento de la función lineal.
