Logaritmos (4ºESO Académicas)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Logaritmos
Sea 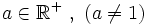 . Se define el logaritmo en base a de un número real
. Se define el logaritmo en base a de un número real 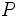 , y se designa por
, y se designa por 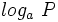 , al exponente
, al exponente  al que hay que elevar la base
al que hay que elevar la base  para obtener
para obtener 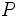 , es decir:
, es decir:
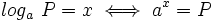
Por consiguiente, podemos ver al logaritmo como la operación inversa de la potenciación.
Logaritmos en su forma exponencial:
Expresa en su forma exponencial equivalente la siguiente expresión logarítmica: 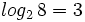
Expresa en su forma exponencial equivalente la siguiente expresión logarítmica: 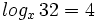
Expresa en su forma exponencial equivalente la siguiente expresión logarítmica: 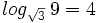
Expresa en su forma exponencial equivalente la siguiente expresión logarítmica: 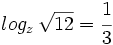
Exponenciales en forma logarítmica:
Expresa en su forma logarítmica equivalente la siguiente expresión exponencial: 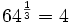
Expresa en su forma logarítmica equivalente la siguiente expresión exponencial: 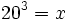
Expresa en su forma logarítmica equivalente la siguiente expresión exponencial: 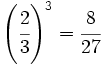
Expresa en su forma logarítmica equivalente la siguiente expresión exponencial: 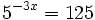
Expresa en su forma logarítmica equivalente la siguiente expresión exponencial: 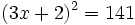
Ejercicios resueltos: Logaritmos
Hallar los siguientes logaritmos reconociendo la potencia correspondiente:
Tutorial que explica la definición de logaritmo y realiza el cálculo de algunos logaritmos exactos (resultado racional) para comprender el significado de esta operación matemática.
- 00:00 a 06:40: Introducción a logaritmo.
- 06:40 a 09:18: Definición de Logaritmo. Explicación.
- 09:18 a 15:52: Ejercicios con Logaritmos (I).
- 14:40 : Logaritmo no exacto.
- 15:52 a 21:03: Ejercicios de Logaritmos (II).
Concepto de logaritmo de un número.
Definición del logaritmo de un número. Ejemplos
Calcula: 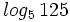
Calcula:
a) 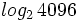 b)
b) 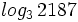 c)
c) 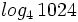 d)
d) 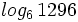
Calcula: 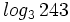
Calcula: 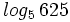
Calcula: 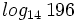
Calcula: 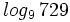
Calcula:
a) 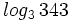 b)
b) ![log_9 \, \sqrt[3]{81}](/wikipedia/images/math/e/3/b/e3bf817a80c0d78b655afb1a5e6e46dd.png) c)
c) 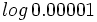 d)
d) 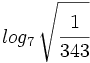 e)
e) 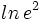
Calcula:
a) 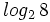 , b)
, b) 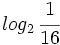 , c)
, c) 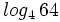 , d)
, d) 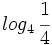
e) 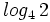 , f)
, f) 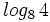 , g)
, g) 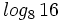 , h)
, h) 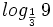
i) 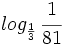 , j)
, j)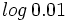 , k)
, k) 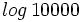 , l)
, l) 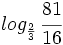
Resuelve:
Propiedades de los logaritmos
Propiedades de los logaritmos:
1: Igualdad y orden:
- a)
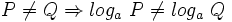 o equivalentemente,
o equivalentemente,
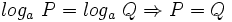
- b)
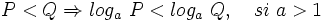
- c)
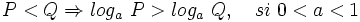
2: Logaritmo de la base:
- a)
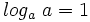
- b)
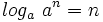
- c)
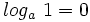
3: Logaritmo de números negativos o nulos:
- Si
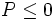 , entonces
, entonces 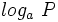 no existe.
no existe.
4: Logaritmo de un producto:
5: Logaritmo de un cociente:
6: Logaritmo de una potencia:
7: Logaritmo de una raíz:
8: Cambio de base:
Tutorial que explica la definición de logaritmo y realiza el cálculo de algunos logaritmos exactos (resultado racional) para comprender el significado de esta operación matemática.
- 00:00 a 03:10: Introducción a logaritmo. Ejercicios de repaso.
- 03:10 a 06:25: Propiedades Básicas.
- 06:25 a 08:30: Propiedad: Logaritmo de un Producto. Demostración.
- 08:30 a 09:20: Propiedad: Logaritmo de una Potencia. Demostración.
- 09:20 a 10:30: Propiedad: Logaritmo de un Cociente. Demostración.
- 10:30 a 13:45: Propiedad: Cambio de Base. Demostración.
- 13:45 a 25:59: Ejercicios de Logaritmos.
Demostración de las propiedades de los logaritmos.
Definición del logaritmo de un número. Propiedades. Ejemplos
Identidad fundamental del logaritmo. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de un producto. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de un cociente. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de una potencia. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de una raíz. Ejemplos de aplicación.
Desarrollo de logaritmos usando las propiedades:
Desarrolla: 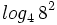
Desarrolla: 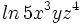
Desarrolla: 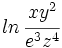
Desarrolla: ![log_e \, \sqrt[4]{e^3x^5} \;](/wikipedia/images/math/9/7/9/979eadabfb3b278c6e762d27ef7878e4.png)
Desarrolla: ![log_3 \, \cfrac{\sqrt[5]{x}}{\sqrt[3]{y}} \;](/wikipedia/images/math/1/6/1/16143fc979664aee83fe3ce7d48fd920.png)
Desarrolla: 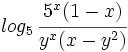
Expresar como un solo logaritmo:
Expresar como un solo logaritmo: 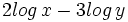
Expresar como un solo logaritmo: 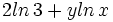
Expresar como un solo logaritmo: 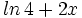
Expresar como un solo logaritmo: 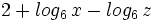
Expresar como un solo logaritmo: 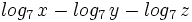
Varios:
Si 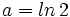 y
y 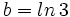 , expresa
, expresa 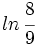 en términos de a y b.
en términos de a y b.
Si 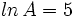 ,
, 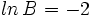 y
y 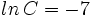 , encuentra el valor numérico de la expresión
, encuentra el valor numérico de la expresión 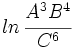 .
.
Escribe como un solo logaritmo: 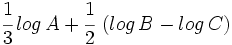 .
.
a) Hallar "m" sabiendo que 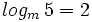 .
.
b) Hallar "x" sabiendo que 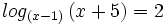 .
.
b) Sabiendo que 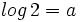 y que
y que 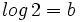 , calcula
, calcula 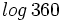 .
.
a) Hallar "x" sabiendo que 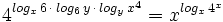 .
.
b) Sabiendo que 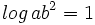 y que
y que 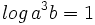 , halla
, halla 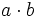 .
.
a) Reduce: 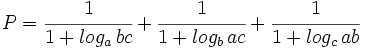 .
.
b) Hallar "x" si 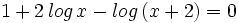 .
.
Desarrolla los siguientes logaritmos:
Reduzca las siguientes expresiones a un solo logaritmo:
Ejercicios:
- Expresa
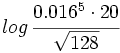 en función de log 2.
en función de log 2.
- Expresa
![log \, \cfrac{12 \sqrt[3]{36}}{\sqrt{0.09^3 \cdot 160}}](/wikipedia/images/math/a/0/3/a03392a26b8add15e65806e0e4e45f6c.png) en función de log 2 y log 3.
en función de log 2 y log 3.
Resuelve:
- Si un número se multiplica por 49, su logaritmo (en base desconocida) aumenta en 2 unidades. Halla la base.
- Resuelve la ecuación
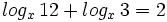
- Determina el menor entero que satisface la condición
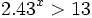
- Determina el mayor real que satisface la condición
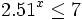
Definición del antilogaritmo de un número. Ejemplos.
Nota: El antilogaritmo es como la inversa del logaritmo, es decir, la exponencial.
Definición de cologaritmo de un número. Ejemplos.
Nota: El cologaritmo es igual al opuesto del logaritmo.
Demostración de la regla de la cadena, una generalización de la fórmula del cambio de base:
Demostración de la regla del intercambio:
a) Calcula:  .
.
b) Halla "x": 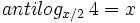 .
.
c) Halla "x": 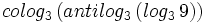 .
.
Logaritmos decimales
Los logaritmos decimales son aquellos de base 10. En vez de representarlos por 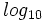 , los representaremos, simplemente, por
, los representaremos, simplemente, por 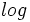 . Esto es:
. Esto es:
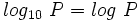
Calculadora
|
Calculadora: Logaritmo decimal |
Antes de la existencia de las calculadoras, los logaritmos decimales se obtenían a partir de las llamadas tablas logarítmicas.
Haciendo uso de la propiedad del cambio de base, vista en un apartado anterior, podemos calcular logaritmos en cualquier base utilizando logaritmos decimales. He aquí un ejemplo:
Ejemplo: Cambio de base
Usa la calculadora para hallar 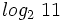 .
.
Como la calculadora científica no tiene logaritmos en base 2, mediante la fórmula del cambio de base haremos un cambio de base 2 a base 10:
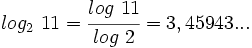
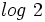 y
y 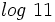 se pueden obtener directamente con la calculadora.
se pueden obtener directamente con la calculadora.Demostración de la fórmula del cambio de base y ejemplos usando la calculadora.
Sin usar la calculadora:
Sin usar la calculadora, calcula: 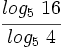
Sin usar la calculadora, calcula: 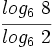
Sin usar la calculadora, calcula: 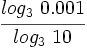
Sin usar la calculadora y teniendo en cuenta que 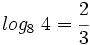 ,
,
calcula: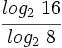
Usando la calculadora:
Calcula: 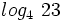
Calcula: 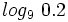
Calcula: 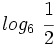
Calcula: 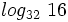
Ejercicios propuestos
|
Ejercicios propuestos: Logaritmos |
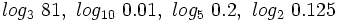
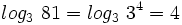
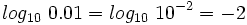
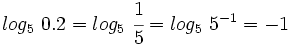
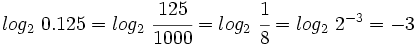
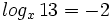
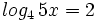
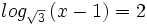
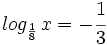
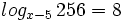
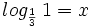
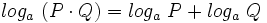
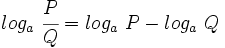
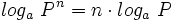
![log_a \ \sqrt[n]{P}=\cfrac{1}{n} \cdot log_a \ P](/wikipedia/images/math/6/c/9/6c919bb3863e8ae2142390b915b8c519.png)
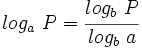
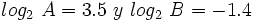 , calcula:
, calcula:
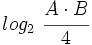
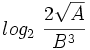
![log_2 \ \cfrac{A \cdot B}{4} \begin{matrix}~_{[5]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ (A \cdot B) - log_2 \ 4=](/wikipedia/images/math/2/6/d/26d0034bc52ab7b3a2b2d941c430aca1.png)
![\begin{matrix}~_{[4]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ A + log_2 \ B - log_2 \ 4=3.5-1.4-2=0.1](/wikipedia/images/math/9/7/0/970be2109f6e4e59d97c656098cb0849.png)
![log_2 \ \cfrac{2 \sqrt{A}} {B^3} \begin{matrix}~_{[5]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ 2 \sqrt{A} - log_2 \ B^3 =](/wikipedia/images/math/0/6/d/06da2c510b8a5216f092a5e9fc5c8b52.png)
![\begin{matrix}~_{[4]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ 2+ log_2 \sqrt{A} - log_2 \ B^3=1+ log_2 \ A^{\frac{1}{2}} - log_2 B^3=](/wikipedia/images/math/0/f/9/0f9259f963826fa4b14149c91a6d5f6b.png)
![\begin{matrix}~_{[6]}~ \\ ~=~ \\ ~ \end{matrix} 1+ \cfrac{1}{2} ~log_2 \ A - 3 \, log_2 \ B=1+ \cfrac{1}{2} \cdot 3.5 - 3 \cdot (-1.4) = 6.95](/wikipedia/images/math/a/8/4/a84d83f66b2b9058af143a2ae4231ef0.png)
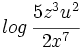
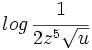
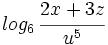
![ln \, \sqrt[3]{\cfrac{x}{z^2u^7}}](/wikipedia/images/math/c/8/5/c851424eddb3c75b5feb58d378224ae7.png)
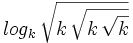
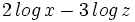
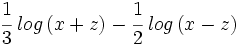
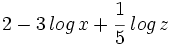
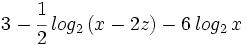
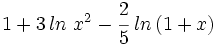
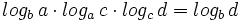
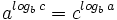
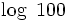
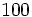

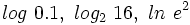 .
.
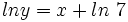 .
.

